[책 요약] 밑바닥부터 시작하는 딥러닝2-Chapter 5. 순환 신경망(RNN)

Intro

지금까지의 신경망은 Feed forward 유형의 신경망이었으나, 이러한 신경망은 시계열 데이터를 잘 다루지 못하는 단점이 있다.
따라서 본 장에서는 시계열 데이터를 다루는데 특화된 RNN이라는 네트워크에 대해서 설명하고자 한다.

확률과 언어 모델

word2vec을 확률 관점에서 바라보다.

word2vec의 경우, 좌우 단어(맥락)을 통해 단어를 유추했다.

이를 확률로 표현하면 다음과 같다.
$$P(w_t|w_{t-1}, w_{t+1})$$
그런데 여기서 만약 왼쪽의 단어들만을 맥락으로 고려하면 어떻게 될까?
$$P(w_t|w_{t-1}, w_{t-2})$$
이것이 바로 언어 모델이다.
- 바닐라 언어 모델은 왼쪽 문맥만을 고려하는 모델(left to right)이라고 봐야하고, 후에 나오는 BERT와 같은 Masked Language Model은 양쪽 문맥을 고려하는 언어 모델이다. 즉 언어 모델의 종류도 다양해서 헷갈릴 수도 있다.

언어 모델

언어 모델(language model)은 단어 나열에 확률을 부여한다. 특정 단어 시퀀스에 대해서 그 시퀀스가 일어날 가능성이 어느 정도 인지(얼마나 자연스러운 단어 순서인지)를 확률로 평가한다.
언어 모델은 다양한 시스템에 응용 가능하다. 예를 들어, 기계 번역과 음성 인식 등이 있다. 음성 인식을 할 때, 이전 음성에서 다음 음성으로 적절한 단어를 판단할 때 이러한 언어모델을 활용할 수 있다.
또한 자연스러운 새로운 문장을 생성하는데도 이용할 수 있다.
언어 모델을 확률로 표현해보자.
- $w_1, ..., w_m$이라는 m개의 단어로 된 문장에서, 단어가 $w_1, ..., w_m$순서로 등장할 확률은 $P(w_1, ... , w_m)$으로 나타내며 여러 사건이 동시에 일어날 확률이므로 동시 확률이라고 한다.
- 이 동시 확률 $P(w_1, ... , w_m)$은 사후 확률을 사용하여 다음과 같이 분해하여 쓸 수 있다.

$$\displaylines{P(w_1, ...,w_m) \\ = P(w_m|w_{1}, ..., w_{m-1})\space P(w_{m-1}|w_{1}, ..., w_{m-2}) \space ... \space \space P(w_{3}|w_{2}w_{1})\space \space P(w_{2}|w_{1}) \space P(w_{1}) \\ = \prod_{t=1}^m{P(w_t|w_1}, ..., w_{t-1})}$$

위 식은 확률의 곱셈정리로 유도 가능하다.
$$P(A,B)=P(A|B)P(B)$$
이 정리가 의미하는 바는 ‘A와 B가 모두 일어날 확률 $P(A, B)$’는 ‘B가 일어날 확률 P(B)’와 ‘B가 일어난 후 A가 일어날 확률 $P(A|B)$’를 곱한 것과 같다는 뜻이다.
이 곱셈정리를 사용하여 m개 단어의 동시 확률 $P(w_1, ...,w_m)$를 사후확률로 표현 할 수 있다.
$$\displaylines{P(A, w_m) = P(w_m|A)P(A) \\ A = w_1, ..., w_{m-1} \\ P(A) = P(A', w_{m-1}) = P(w_{m-1}|A')P(A') \\ ...}$$
위처럼 한단계씩 줄여가면서 사후 확률로 분해해갈 수 있다.

지금까지의 이야기를 정리하면, 최종 목표는 $P(w_t|w_1, w_2, ..., w_{t-1})$ 을 구하는 것이고, 이 확률을 계산하면 $P(w_1, w_2, ..., w_{t-1}, w_t)$ 를 구할 수 있다.
위의 확률을 나타내는 모델을 조건부 언어 모델 혹은 언어 모델이라고 한다.

CBOW 모델을 언어 모델로?

CBOW와 같은 word2vec 모델을 억지로 언어 모델로 바꿀 수 있다. contexts를 왼쪽 일부 단어로 고정하고 근사하면 된다.
$$P(w_1, ..., w_m)=\prod_{t=1}^m{P(w_t|w_1}, ..., w_{t-1}) \approx \prod_{t=1}^m{P(w_t|w_{t-2}}, w_{t-1})$$

위 식처럼 미래의 상태가 현재 상태에만 의존하는 것을 마르코프 연쇄라고 한다. 여기서는 직전 2개의 단어에만 의존해 다음 단어가 정해지는 모델이므로 ‘2층 마르코프 연쇄’라고 부를 수 있다.

여기서는 맥락을 2개로 고정했으나 맥락의 크기는 임의 길이로 변경 할 수 있다. 그러나 결국 특정 길이로 고정되기 때문에 한계가 존재한다.
또한 맥락 안의 단어 순서가 무시된다. (you, say) 나 (say, you)나 동일한 입력으로 취급된다(평균)
이를 보완하기 위해 입력 단어들을 concat하여 은닉층에 연결하는 방식(Neural Probabilistic LM)이 제안되었으나, concat하는 방식을 취하면 맥락의 크기에 비례해 가중치 매개변수도 늘어난다.

따라서 이러한 단점(맥락 길이 제한, 순서 무시)을 극복하기 위해 RNN이 등장한다 (사실 RNN은 2010년, CBOW 모델은 2013년에 제안되었음)

RNN이란

RNN(recurrent Neural Network)의 Recurrent는 라틴어에서 온 말로, ‘몇 번이나 반복해서 일어나는 일’을 뜻하며 ‘재발한다, 주기적으로 일어난다, 순환한다’ 등으로 번역 가능.
RNN을 직역하면 ‘순환 신경망’이 됨

순환하는 신경망

RNN에서는 무엇이 순환할까? RNN에서는 정보가 순환한다. 여기서 정보라 함은, 이전 문맥, 즉 이전에 등장했던 단어들에 대한 정보가 순환된다.
여기서 정보가 순환되기 위해서는 ‘순환 경로(닫힌 경로)’가 필요하다.

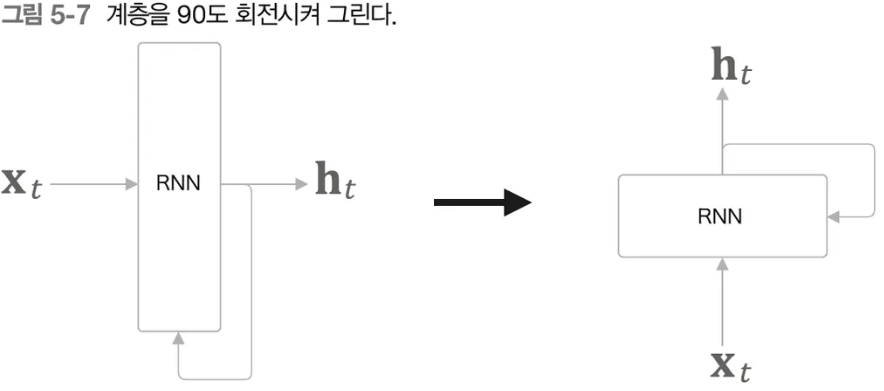
RNN을 처음 공부하면 위 그림이 전혀 이해가 안된다. t 시점에 대한 그림이기 때문에 그렇다. 반드시 0시점부터 t시점까지 전체 프로세스를 봐야 이해가 된다.

순환 구조 펼치기

RNN의 순환 구조를 펼치면 익숙한 신경망 구조로 이해할 수 있다.

지금까지 봐왔던 Feed Forward Network와 유사하게 정보가 앞층에서 뒤층으로 흐르는 구조이지만 여기서는 모든 층이 동일한 네트워크라는 것이 다르다.

시계열 데이터는 시간 방향으로 데이터가 나열되기 때문에 시계열 데이터의 인덱스를 가리킬 때는 ‘시각, 시점’이라는 표현을 사용함

위 그림에서 보듯, RNN 계층은 현재 t시점의 입력($\textbf{x}t$)과 이전 시점의 출력($\textbf{h}{t-1}$)을 입력으로 받는다. 이를 수식으로 나타내면 다음과 같다.(입력과 출력은 모두 행 벡터)
$$\textbf{h}_t = tanh(\textbf{h}_{t-1}\textbf{W}_\textbf{h} + \textbf{X}_{t}\textbf{W}_\textbf{x}+\textbf{b})$$
RNN에는 2개의 가중치가 있다.
- $\textbf{W}_\textbf{h}$$: 이전 시점의 출력을 받아서 현재 시점의 출력으로 변환하기 위한 가중치
- $\textbf{W}\textbf{x}$ : 현재 시점 입력 $\textbf{X}{t}$를 $\textbf{h}$로 변환하기 위한 가중치
- $\textbf{b}$ : 편향
- tanh: activation function. 여기서 갑자기 ReLU를 쓰지 않고 tanh를 쓰는 이유는, RNN은 기본적으로 여러번 재귀적으로 값을 곱해나가는데, ReLU를 쓰게 되면 쉽게 gradient explosion이 발생하기 쉽다(1이상의 값을 계속 곱해나가면 순식간에 값이 커짐, 링크)

tanh를 통과한 $\textbf{h}_t$ 는 다른 계층을 향해 위로 출력됨과 동시에 다음 시점 계산을 위해 오른쪽(자기자신)으로도 출력 됨
- Multi-layer RNN이면 RNN 위에 또 RNN이 있으므로 그 때 사용될 수도 있음
- RNN with Attention이면 Attention을 위해 계산이 되기도 한다.
위 식을 보면 $\textbf{h}t$는 $\textbf{h}{t-1}$에 기초하여 계산됨을 알 수 있다. 이를 다른 관점에서 보면, RNN은 $\textbf{h}$라는 ‘상태’를 가지고 있고, 위 식대로 매번 갱신됨을 알 수 있다.
그래서 RNN을 ‘상태를 가지는 계층’ 혹은 ‘메모리(기억력)가 있는 계층’이라고 한다.
- 사실 멀티레이어 신경망에서도 k 번째 층의 출력을 ‘상태’로 표현 할 수도 있기 때문에 상태를 가진 다는 말은 RNN만의 특징으로 설명하기 모호하다. 이 상태가 시점 정보를 담은 것임을 유의해야 한다.

RNN의 $\textbf{h}$는 ‘상태’를 기억해 시각이 1 스텝 진행될 때마다 갱신된다. 많은 문헌에서 RNN의 출력 $\textbf{h}$를 은닉 상태(hidden state) 혹은 은닉 상태 벡터(hidden state vector)라고 한다.

BPTT

RNN 계층의 오차 역전파 모습을 그리면 다음과 같다.

여기서의 오차연전파 법은 ‘시간 방향으로 펼친 신경망의 오차역전파법’이란 뜻으로 BPTT(Backpropagation Through Time)이라고 한다.
BPTT를 이용해 기울기를 구하려면, 매 시간 RNN 계층의 중간 데이터를 메모리에 유지해둬야 한다. 따라서 시계열 데이터가 길어짐에 따라 계산량과 메모리 사용량도 증가하게 된다.

Truncated BPTT

너무 길어진 신경망을 적당한 지점에서 잘라내어 신경망 여러 개로 만든다는 아이디어
TBPTT는 신경망의 연결을 끊지만 제대로 구현하려면 역전파의 연결만 끊어야 한다.
순전파의 연결은 반드시 그대로 유지해야 한다.

첫 번째 블록: 먼저 순전파를 수행하고, 그 다음 역전파를 수행한다.

두 번째 블록: 순전파 계산시 앞에서 받은 $\textbf{h}_9$을 이용하여 순전파를 계산, 그 다음 역전파 수행

세 번째 블록도 마찬가지로 구현 가능
- 여기까지의 내용만 읽어보면 잘 이해가 가지 않는다. 신경망을 잘라서 따로 학습을 한다고 할 때, 어쨌든 각 블록의 역전파 계산시에 다음 블록에서 전달해온 미분값이 필요하다.
  → 틀렸다. 다음 블록의 역전파는 필요하지 않다. 왜냐하면 Loss를 블록 단위(정확히는 매 타임스텝 마다)로 계산하기 때문이다.
전체 순서를 보면 다음과 같다.

Truncated BPTT의 미니 배치 학습

만약 길이가 1000개인(즉, 1000글자 짜리 글)을 학습한다고 하면 어떻게 해야할까?
배치 사이즈를 2로 하면 500개씩 잘라서 0~499 → batch1, 500~999 → batch2에 담는다.
- 이렇게 할 경우, batch 2를 계산할 때 batch 1의 정보를 담을 수 없기 때문에 문제가 생긴다. 그러나 책에서는 이러한 것에 대한 언급이 없다.
그리고 각 샘플은 Truncated BPTT를 위해 10개씩 잘랐다고 하면 다음 그림처럼 된다.

책에는 이렇게까지 설명이 되어 있지만, 이렇게 할 경우 궁금한 점이 생긴다.
- TBPTT에서도 순전파를 하기 위해선 이전 블록의 $\textbf{h}$가 필요한데, 그렇다면
- batch 1에선 0~9 순전파 → 10~19 순전파 → … → 490~499 순전파
- batch 2에선 500~509 순전파 → 510~519 순전파 → … → 990~1000 순전파
- 이렇게 된다는 건데, 그럼 병렬처리가 전혀 안되는거고 배치는 backprop 할 때나 배치의 효과가 있지, 순전파 시에는 배치가 가져오는 병렬처리 효과는 거의 없다고 봐야되나?
- 혹은 블록 간의 $\textbf{h}$가 전달 되는 부분은 모두 제거 할 수도 있다
- 또는 cnn처럼 한글자씩 우측으로 stride 해나가는 샘플로 구현하면 블록 간의 연결이 끊기는 부작용을 조금 덜 수도…

RNN 구현

RNN 계층 구현

RNN 계층을 수식으로 표현하면 아래와 같다
$$\textbf{h}_t = tanh(\textbf{h}_{t-1}\textbf{W}_\textbf{h} + \textbf{X}_{t}\textbf{W}_\textbf{x}+\textbf{b})$$
이 때 가중치와 입력 벡터간 차원은 아래와 같이 맞춰줘야 한다.

RNN 계층의 순전파를 계산 그래프로 나타내면 다음과 같다.

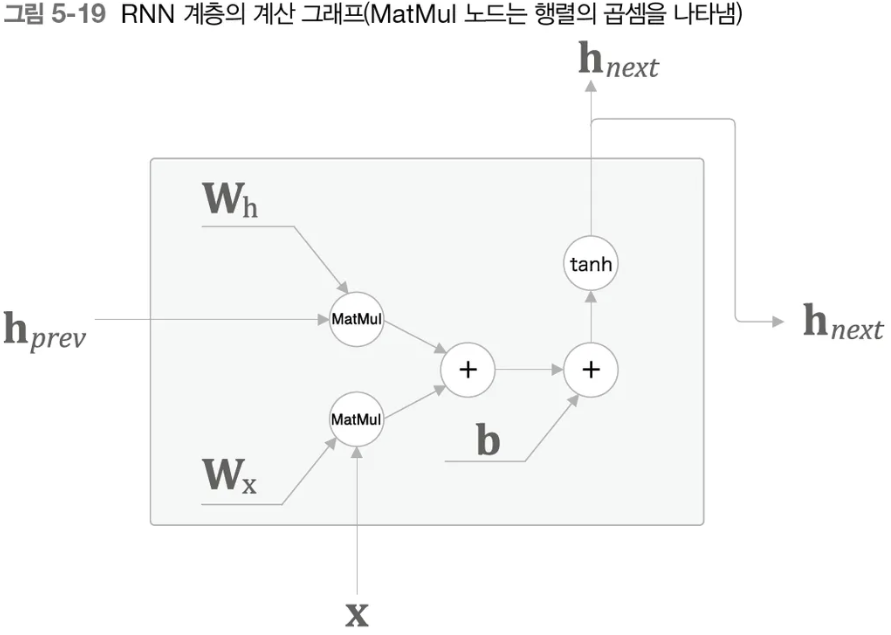
역전파는 다음과 같다.

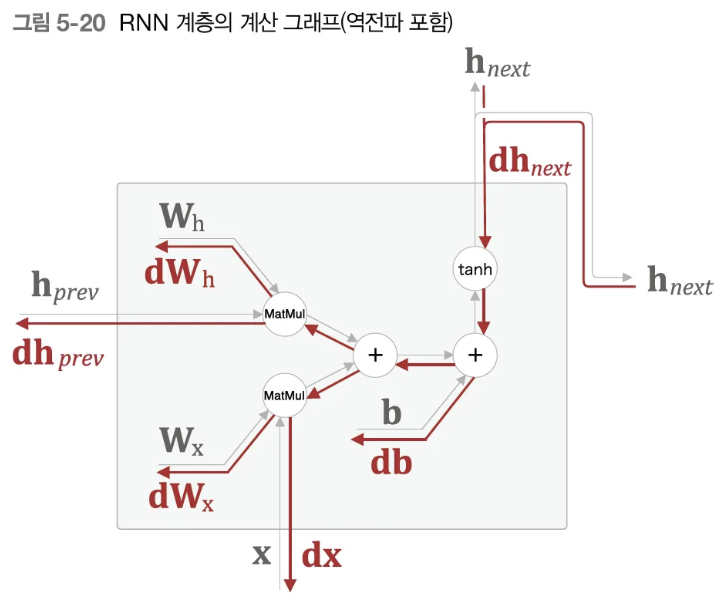
지금까지와는 달리 이 그림에서는 $\partial L$ 로 표현되지 않고 d로 표현한다. 아직 Loss를 구하는 로직을 설명하지 않아서 인 것 같다.

Time RNN 계층 구현

Time RNN은 T개의 RNN 계층으로 구성된다.(TimeRNN은 이 책에서만 사용되는 용어)

Time RNN에서는 각 RNN 계층의 $\textbf{h}$를 저장하고 다음 RNN 계층으로 인계하는 작업을 한다.

def forward(self, xs):
    Wx, Wh, b = self.params
    N, T, D = xs.shape
    D, H = Wx.shape
	
    self.layers=[]
    hs = np.empty((N, T, H), dtype='f')
	
    if not self.stateful or self.h is None:
        self.h=np.zeros((N, H), dtype='f')
	
    for t in range(T):
        layer = RNN(*self.params)
        self.h = layer.forward(xs[:,t,:], self.h)
        hs[:, t, :] = self.h
        self.layers.append(layer)
		
    return hs

위의 TimeRNN의 forward 함수를 보면, 특이한 점이 있는데 forward 함수 내에서 layer를 Time step 별로 새로 만드는 것이다.
- 이는 나중에 Time step 별로 backprop을 계산하기 위함인듯 싶다. 왜냐하면 forward 과정에서는 W값이 변하지 않기 때문에 RNN(*self.parms)를 해도 다 똑같은 RNN만 만들어지기 때문이다.
Time RNN의 역전파 구현
- 상류쪽에서 전해지는 기울기를 dhs로 쓰고, 하류로 내보내는 기울기를 dxs
- Truncated BPTT를 수행하기 때문에 이 블록의 이전 시각 역전파는 필요하지 않다. 단, 이전 시각의 은닉 상태 기울기는 인스턴스 변수 dh에 저정해 둔다.(뒤에 seq2seq 파트에서 사용)

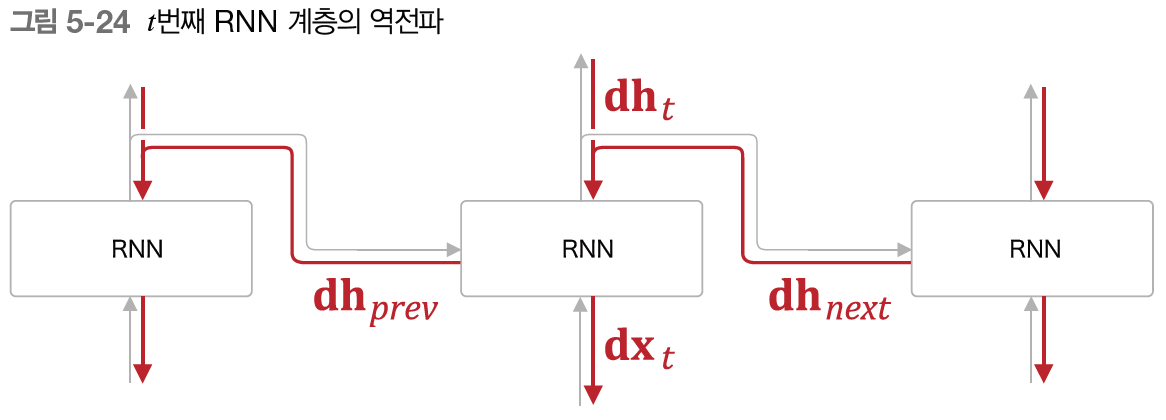
t번째 RNN 계층에서는 위로부터의 기울기 $\textbf{dh}t$와 한 시점 뒤(미래)의 기울기 $\textbf{dh}_{next}$가 전해진다.
즉, 합산된 기울기 ($\textbf{dh}_t + \textbf{dh}_{next}$) 가 입력된다.
Time RNN 계층의 backward 함수는 다음과 같다

def backward(self, dhs):
    Wx, Wh, b = self.params
    N, T, H = dhs.shape
    D, H = Wx.shape
	
    dxs = np.empty((N, T, D), dtype='f')
    dh = 0
    grads = [0, 0, 0]
    for t in reversed(range(T)):
        layer = self.layers[t] # t 시점의 RNN 레이어(근데 결국 다 똑같은데...)
        dx, dh = layer.backward(dhs[:, t, :] + dh) # 합산된 기울기
        dxs[:, t, :] = dx
		
        for i, grad in enumerate(layer.grads):
            grads[i] += grad
	
    for i, gard in enumerate(grads):
        self.grads[i][...] = grad
    self.dh = dh
	
    return dxs

시계열 데이터 처리 계층 구현

이제 RNN을 사용하여 ‘언어 모델’을 구현해보자
RNN + 언어모델(LM) = RNNLM 이라 칭함

RNNLM의 전체 그림

맨 아래 Embedding 계층에선 단어 index를 입력으로 받아서 단어의 분산 표현(단어 벡터)로 변환한다.
RNN 계층은 입력된 단어 벡터와 이전 시점의 은닉 상태를 받아서 계산 후, 위와 옆(다음 시점)으로 출력한다.
위로 흐른 은닉 상태는 Affine 계층과 softmax 계층을 거쳐서 최종 출력을 내보낸다
간단한 입력에 대한 처리 예시

각 시점의 softmax 계층의 출력이 맥락에 맞는 단어를 맞추기 위해서, RNN 레이어는 이전 시점의 맥락(은닉 상태 벡터)을 기억하고, 이러한 정보를 현 시점의 정보와 더불어 Affine, Softmax 레이어에 전달한다.
이처럼 RNNLM은 지금까지 입력된 단어를 ‘기억’하고 그것을 바탕으로 다음에 출현할 단어를 예측합니다. 이 일을 가능하게 하는 비결이 바로 RNN 계층의 존재이다. RNN 계층이 과거에서 현재로 데이터를 계속 흘려보내줌으로써 과거의 정보를 인코딩해 저장(기억)할 수 있는 것이다.

최종 로스

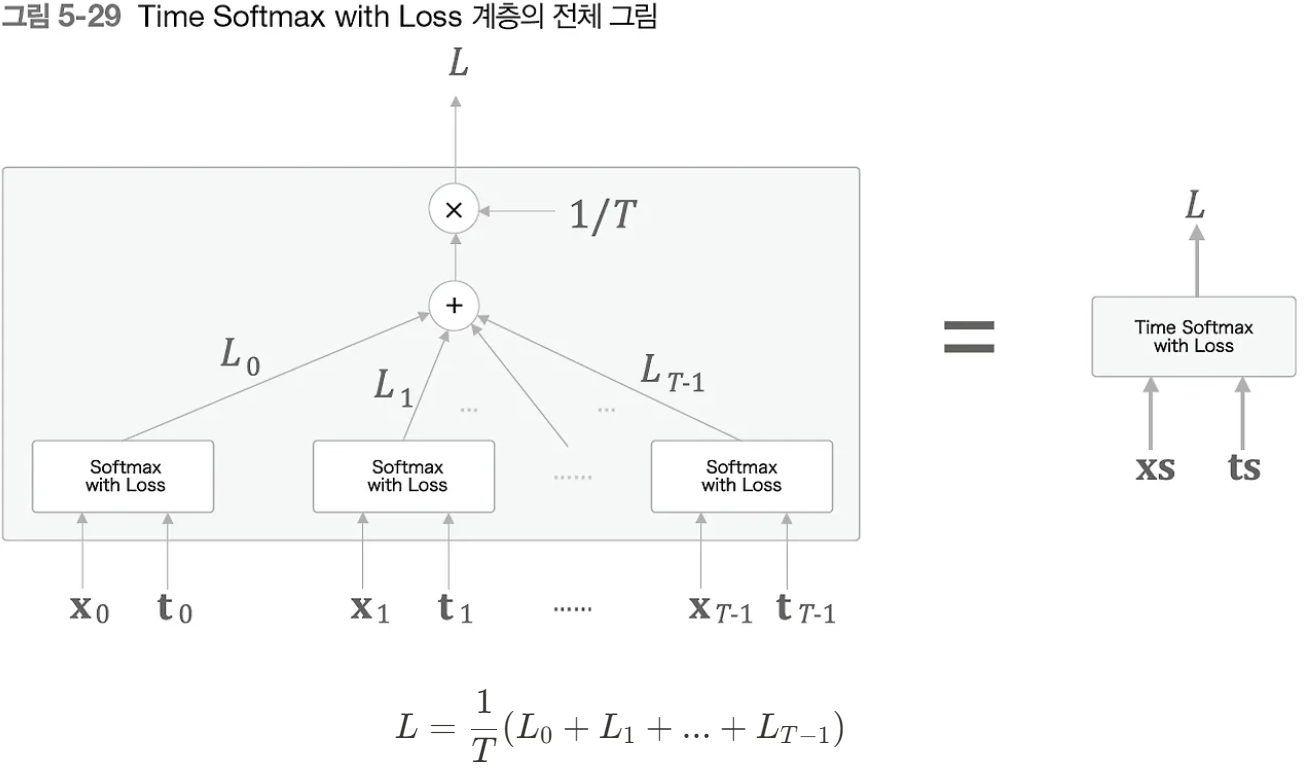
언어 모델의 평가

언어 모델의 예측 성능을 평가하는 척도로 Perplexity, 혼란도를 자주 사용한다.
Perplexity는 간단히 말하면 ‘확률의 역수’이다.
아래와 같은 그림에서, 모델2가 훨씬 다음에 출현할 단어를 헷갈리고 있다고 볼 수 있다.

모델1이 정답을 뱉을 확률이 0.8, 모델 2는 0.2라면 역수는 각각 $\frac{1}{0.8}=1.25, \space \frac{1}{0.2}=5$ 이다.
따라서 Perplexity가 작으면 좋다는 것을 알 수 있다.
이러한 값은 직관적으로 ‘분기 수(number of branches)’로 해석 할 수 있다. 즉, 다음에 취할 수 있는 선택사항의 수(단어의 후보)이므로, 작을 수록 덜 헷갈리고 있다고 볼 수 있다.
입력 데이터가 여러개일 경우 다음과 같이 계산한다.

$$L = -\frac{1}{N}\sum_n\sum_k t_{nk} \log y_{nk}$$

N은 데이터의 총 개수, $t_n$은 원핫벡터로 나타낸 정답 레이블이며, $t_{nk}$는 n개째 데이터의 k번쨰 값이다. $y_{nk}$는 softmax의 출력인 확률 분포를 나타낸다
위 식은 사실 교차 엔트로피 로스 식과 완전히 동일한 식이며, 이를 사용해 $e^L$을 계산한 값이 곧 Perplexity이다.

정리

RNN은 순환하는 경로가 있고, 이를 통해 내부에 ‘은닉 상태’를 기억할 수 있다.
RNN의 순환 경로를 펼침으로서 다수의 RNN 계층이 연결된 신경망으로 해석할 수 있으며, 보통의 오차 역전파법으로 학습할 수 있다(=BPTT)
긴 시계열 데이터를 학습할 때는 데이터를 적당한 길이씩 모으고(이를 ‘블록’이라고 한다). 블록 단위로 BPTT에 의한 학습을 수행한다(=Truncated BPTT)
Truncated BPTT에서는 역전파의 연결만 끊는다.
Truncated BPTT에서는 순전파의 연결을 유지하기 위해 데이터를 ‘순차적으로’ 입력해야 한다.
언어 모델은 단어 시퀀스를 확률로 해거한다.
RNN 계층을 이용한 조건부 언어 모델은 이론적으로는 그때까지 등장한 모든 단어의 정보를 기억 할 수 있다.

'인공지능 > [책] 밑바닥부터 시작하는 딥러닝2' 카테고리의 다른 글

[책 요약] 밑바닥부터 시작하는 딥러닝2-Chapter 7. RNN을 사용한 문장 생성 (0)	2024.11.12
[책 요약] 밑바닥부터 시작하는 딥러닝2-Chapter 6. LSTM(게이트가 추가된 RNN) (0)	2024.11.12
[책 요약] 밑바닥부터 시작하는 딥러닝2-Chapter 4. word2vec 속도 개선 (0)	2024.11.11
[책 요약] 밑바닥부터 시작하는 딥러닝2-Chapter 3. word2vec (1)	2024.11.11
[책 요약] 밑바닥부터 시작하는 딥러닝2-Chapter 2. 자연어와 단어의 분산 표현 (0)	2024.11.11