자연어 처리란
- 한국어와 영어 등 우리가 평소에 쓰는 말을 자연어라고 하며, 이러한 자연어를 컴퓨터에게 이해시키기 위한 기술이다.
- 우선 ‘단어의 의미’부터 살펴보자
시소러스
- 시소러스란 유의어 사전으로, 뜻이 같은 단어(동의어)나 뜻이 비슷한 단어가 한 그룹으로 분류되어 있다.
- 자연어 처리에 이용되는 시소러스에서는 단어 사이의 ‘상위와 하위’ 혹은 ‘전체와 부분’ 등 서로의 관계에 기초해 표현된다.

- 이러한 네트워크를 통해서 컴퓨터에게 단어 사이의 관계를 입력시킬 수 있다.
WordNet
- 자연어 처리에서 가장 유명한 시소러스는 WordNet이다. 프린스턴 대학교에서 1985년부터 구축하기 시작한 전통 있는 시소러스이다.
시소러스의 문제점
- 시대 변화에 대응하기 어렵다
- 언어는 계쏙 바뀌고 새로운 단어가 생성된다. 그럴때마다 사람이 수작업으로 갱신해야 한다.
- 사람을 쓰는 비용이 크다
- 현존하는 영단어는 1000만개가 넘는다. 이러한 단어들에 대해 관계를 사람이 일일이 정의하기 쉽지 않다
- 단어의 미묘한 차이를 표현할 수 없다.
- 빈티지 vs 레트로와 같이 뜻은 같으나 미묘한 쓰임의 차이를 갖는 단어를 잘 표현하기 어려움
통계 기반 방법
- Corpus: 말뭉치, 대량의 텍스트데이터
- 단어의 분산 표현: 색을 RGB 세가지 값으로 된 벡터로 표현 할 수 있듯이, ‘단어의 의미’를 벡터로 표현 할 수 있다. 이를 단어의 분산 표현(distributional representation)이라고 한다.
분포 가설
- 자연어 처리 역사에서 가장 중요한 가설: ‘단어의 의미는 주변 단어에 의해 형성된다’ → 분포가설

동시발생 행렬
- 주변에 등장하는 단어를 세어 집계하는 방법 → 통계 기반 기법
- ‘the quick brown fox jumps’ 문장에 대한 co-occurence matrix

벡터 간 유사도
- 벡터 사이의 유사도를 측정하는 방법은 다양하다. 대표적으로 벡터의 내적이나 유클리드 거리 등이 있다.
 코사인 유사도 공식
코사인 유사도 공식
- 분자에는 백터의 내적이, 분모에는 각 벡터의 노름(norm)이 등장한다. 여기서는 L2노름 사용
- 위 식의 핵심은, 벡터를 정규화하고 내적을 구하는 것
- 코사인 유사도를 직관적으로 해석하면, ‘두 벡터가 가리키는 방향이 얼마나 비슷한가’ 이다.
- 두 벡터의 방향이 완전히 같다면 1, 정반대라면 -1이 된다(0이면 90도)
- 참고로 외적의 의미는 두 벡터가 얼마나 수직한지를 의미
def cos_sim(x,y):
nx = x / np.sqrt(np.sum(x**)) # x 정규화
ny = y / np.sqrt(np.sum(y**)) # y 정규화
return np.dot(nx, ny)
통계 기반 기법 개선하기
상호 정보량
- 발생 횟수만으로 판단하게 되면 ‘the’와 ‘car’는 의미상 관련이 없지만 강한 상관성을 가지는 것으로 나오게 됨
- 이 문제를 해결하기 위해 점별 상호정보량(Pointwise Mutual Information)을 사용
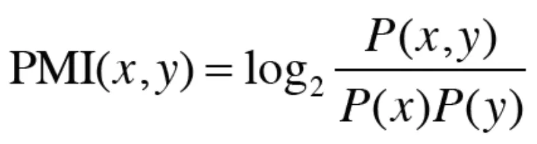
- P(x) = x가 일어날 확률, P(x,y)= x, y가 동시에 일어날 확률
- 확률을 횟수로 바꿔 표현하면 아래와 같다.

- 위 식대로 ‘the’, ‘car’와 ‘car’, ‘drive’의 PMI를 계산해보면,

- 위처럼 reasonable하게 값이 나오는 걸 확인 가능
- 단, 동시발생 횟수가 0이면 \(log_20 = -inf\) 이므로, 양의 상호정보량(Positive PMI)를 사용
- \(PPMI(x,y)=max(0, PMI(x, y))\)
- 발생 횟수 대신 PPMI로 표현한 행렬

- 이런 PPMI 행렬도 어휘 수가 10만개라면 벡터의 차원도 10만개가 된다. 게다가 대부분의 원소도 0으로 채워져있다. 그만큼 비효율적이면서 노이즈에 약한 단점이 있다.
차원 감소
- dimensionality reduction은 말 그대로 벡터의 차원을 줄이는 방법이다. 단, ‘중요한 정보’는 최대한 보존한 채로 줄이는게 핵심이다.
 2차원 데이터를 1차원으로 표현하기
2차원 데이터를 1차원으로 표현하기
- 2차원 데이터를 1차원으로 표현할 경우, 1차원 값만으로도 데이터의 본질적인 차이를 구별할 수 있어야 한다.
특이값분해(Singular Value Decomposition, SVD)

- SVD는 임의의 행렬을 세 행렬의 곱으로 분해한다.
- \(\mathbf{X = USV^T}\)
- U와 V는 직교행렬(orthogonal matrix)이다.
- 직교행렬: 정방행렬로, \(\mathbf{QQ^T=I}\)이다.
- S는 대각행렬(diagonal matrix)이다(대각성분 외에 모두 0)
- U는 직교행렬이다. 직교행렬은 어떠한 공간의 축(기저)를 형성한다.
- 자연어처리 맥락에서는 이 U 행렬을 ‘단어 공간’으로 취급할 수 있다.
- 또한 S는 대각행렬로, 그 대각성분에는 ‘특잇값 singular value’이 큰 순서로 나열되어 있다. 특잇값이란, 쉽게 말해 ‘해당 축’의 중요도라고 간주 할 수 있다.
- 그래서 다음과 같이 중요도가 낮은 원소를 깎아내는 방법을 생각해 낼 수 있다.

- 행렬 S에서 특잇값이 작다면 중요도가 낮다는 뜻이므로, 행렬 U에서 여분의 열벡터를 깎아내어 원래의 행렬을 근사 할 수 있다.
- SVD를 직접 해본 결과, goodbye와 hello가 가까이 있고, i와 you가 가까이 있는 것을 볼 수 있다.

PTB 데이터셋
- Penn Treebank라는 말뭉치를 사용할 수 있다. word2vec의 저자 토마스 미콜로프의 웹페이지에서 다운로드 가능하다.
- PTB데이터셋에 통계 기반 기법(Truncated SVD)를 적용하면 다음과 같다.

- query와 제법 유사한 단어들이 검색되는 것을 볼 수 있다.
정리
- WordNet 등의 시소러스를 이용하면 유의어를 얻거나 단어 사이의 유사도를 측정하는 등 유용한 작업을 할 수 있다.
- 시소러스 기반 기법은 시소러스를 작성하는 데 엄청난 인적 자원이 들고 새로운 단어에 대응하기 어렵다.
- 현재는 말뭉치를 이용해 단어를 벡터화하는 방식이 주로 쓰인다.
- 최근의 단어 벡터화 기법들은 대부분 ‘단어의 의미는 주변 단어에 의해 형성된다’는 분포 가설에 기초한다.
- 통계 기반 기법은 말뭉치 안의 각 단어에 대해서 그 단어의 주변 단어의 빈도를 집계한다(동시발생 행렬)
- 동시발생 행렬을 PPMI 행렬로 변환하고 다시 차원을 감소시킴으로써, 거대한 ‘희소벡터’를 작은 ‘밀집벡터’로 변환할 수 있다.
- 단어의 벡터 공간에서는 의미가 가까운 단어는 그 거리도 가까울 것으로 기대된다.