[강의 요약] 패캠 시계열 분석 - Part1. 데이터 분석 첫 걸음 떼기

Intro

최근 다시 코인 열풍이 불면서, AI로 코인 가격 예측을 해보고 싶다는 생각이 들었다. 그래서 패캠에서 시계열 분석 강의를 찾아서 내돈내산으로 수강했다.

내용 자체는 쉽고 기초적인 내용으로 광범위하게 구성되어 있어서 좋았으나, 실무에 적용할 만큼 유용한 정보라든가 강의 퀄러티가 높다거나 그러지는 않았다.. 결론적으로 비추한다..

Ch2. 데이터 분석 소개

데이터 분석의 범위

기술통계(Descriptive Statistics)
- 주어진 데이터의 분포나 빈도, 평균 등의 통계량을 통해서 데이터를 설명
  - ex) 대한민국 성인 남성의 평균 키
- 현상 설명 → 모집단(population) vs 표본(sample)
추론통계(Inferential Statistics)
- 모집단에서 추출된 표본으로 부터 모수와 관련된 통계량들의 값을 계산하고, 이것을 이용하여 모집단의 특성을 알아내는 과정(검증)
- 가설 검정 → 예측의 영역
주요 용어
- 모수(parameter): 모집단 분포 특성을 규정 짓는 척도(like 평균, 분산)
  - c.f. 모수 검정(parametric test) vs 비모수 검정(non-parametric test)
    - 모수 검정: 모집단이 정규성을 갖는다는 특성을 활용하여 표본을 대상으로 도출된 평균, 분산 등으로 모집단의 특성을 유추하며, 이를 모-표준편차, 모-분산 등이라 부르고 한번에 모수(parameter)라고 지칭
    - 비모수 검정: 모수 검정과 달리, 정규분포를 가정하지 않기에 평균, 표준편차 등이 없다. 표본크기가 작을 경우에 계산이 복잡하지 않는 다는 장점. 검정통계량의 신뢰성이 떨어짐.
  - c.f. 빈도주의(frequentist) vs 베이지안(Bayesian)
    - 빈도주의: 참된 확률값은 고정된 상수이며, 데이터로 이 상수를 검증하자는 주의
    - 베이지안: 참된 확률값은 상수가 아닌 분포로 존재하는 변수이며, 데이터를 설명하는 변수를 찾아내자는 주의
  - c.f. 초모수, 초매개변수(hyperparameter, 하이퍼 파라미터) → 머신러닝의 중요개념
- 추정(estimation)

통계적 가설 검정

통계적 가설 검정의 5단계
- 유의수준의 결정, 귀무가설(H0)과 대립가설(H1) 설정
- 표집(sampling) 및 검정통계량의 설정
  - 랜덤, 층화, 스노우볼 샘플링 등
- 기각역의 설정
- 검정통계량 계산 및 영가설 확인
- 통계적인 의사결정

먼저 나의 가설을 통계적 가설로 바꾸어 보자.

귀무 가설(H0): 우리나라 여성의 평균 키는 180 cm 이다.
대립 가설(Ha): 우리나라 여성의 평균 키는 180 cm 이 아니다.
검정(예시 1)
- H0: μ = 180 (양측검정, two-tailed test)
- H1: μ > 180 (단측검정, one-tailed test)
- H1: μ < 180 (단측검정, one-tailed test)
주요 개념
- p-value, Significance Level, Confidence Level

P-Value(probability value): 어떤 사건(귀무가설)이 우연히 일어날 확률. 따라서 이 값이 매우 작다면 어떤 사건이 우연히 일어날 확률이 매우 작다는 의미이므로 영가설을 기각한다. 그래서 영가설은 어떤 사건이 우연히 일어날 수 있거나 서로 연관관계가 없다 등으로 가설을 만든다. 예를 들어, 이 약은 효과가 없다(즉, 우연한 효과로 몸이 좋아졌다), 한국인과 일본인의 키 차이가 별로 없다 등의 가설을 만들 수 있다.
- p-value는 귀무가설이 일어날 사건의 확률이라고 봐야한다.(우연히 사건이 일어날 확률)
- P-value가 크면 귀무가설이 참
- P-value가 작으면 귀무가설 기각
참고
- T-test (표본집단 평균에 대한 검정)
- F-test (표본집단 분산에 대한 검정)

예측 모델이란?

기본 가정: $y = aX + b$
회귀 모델: 예측하고자 하는 변수(y)가 연속적이면,
- "평균으로의 회귀(Regression toward the mean)"
- 선형: Linear Regression
- 비선형: Polynomial (Cubic) Regression, Generalized Linear Model (GLM), Generalized Additive Model (GAM), Spline 등
분류 모델: 예측하고자 하는 변수(y)가 이산적이면,
- 선형 기반: Linear Probability Model, Logistic Regression (--> Softmax Classifier), Support Vector Machines (SVM)
- 트리 기반: Decision Tree, Bagging, Boosting, Random Forest 등 --> 머신러닝(Part 2)에서 다시 다룰 예정
c.f. 분류
- 이진분류 vs 다중분류 --> 딥러닝(Part 5)에서 다시 다룰 예정
Prediction : 통계적 검정
Forcasting: 시계열에서는 주로 이 용어를 씀

시계열 모델이란?

(y = aX_i + t_i + b\)
- 관측시간 $t_i$에 대한 관측자료 $x_i$ 의 관계로 표현
  - 관측시간 $t_i$를 왜 더하냐;;;
- 수리통계학, 전파공학, 딥러닝의 방법론 차용
시계열 분석의 유용성
- 데이터를 발생 순서대로 배열함으로써 몰랐던 사실을 발견
- 동일 기간 동안 다른 관찰 대상의 차이 분석
- 시기별 데이터의 차이를 정량화(YoY, QoQ, MoM 등)
- 구간별 데이터 추이를 포착(상승-하락구간, 확장-수축국면)
- 특정 사건의 반복 패턴과 발생빈도를 확인
시계열 분석시 주의점
- 자기상관(autocorrelation)에서 자유로울 수 없음
  - 내가 이해한건 마치 마르코프 처럼, 현재 값이 이전 값에서 자유로울 수 없다는 의미??
  - 자기 상관이 있는 자료는 일반적인 방법으로 표준편차를 구하면 작게 측정되어 관리 한계가 좁아지게 됨
- 빈약한 자료(Unbalanced panel data)와 데이터간 연관성
- 예측(prediction)과 예측(forecasting): 수리적 통계모형에 의한 인과관계 vs 시간의 상관관계를 이용한 그 다음 시간(t+1)의 추정치 획득
- 시계열 분석에서 데이터의 처리는? 유의수준의 측정은?
시계열 방법론의 데이터 사이언스 활용 현황
- 시장상황을 반영한 자산배분 알고리즘
- 모션센서 수집 데이터를 이용한 활동 추천
- 모빌리티 패턴을 이용한 신용도 프로파일링
- 택배 물동량 추이를 이용한 소비심리 예측

Ch3. 시계열 데이터 살펴보기

시계열 데이터의 주요 형태

시계열 데이터의 시각화

R의 monthplot 사용
각 데이터의 같은 시점(월) 데이터를 모은 것

각 월별 데이터를 모으면 값이 서로 비슷하고, 점점 향상된 다는 것을 알 수 있음
직선은 평균
TS에서 많이 쓰이는 데이터

Ch 4. 시계열 데이터와 친해지기

차분(Difference): diff

데이터를 정상으로 바꾸는 방법은 무엇일까?
- 차분(Differencing)이란, 현 시점 데이터에서 d시점 이전 데이터를 뺀 것을 의미합니다. 정상성을 나타내지 않는 시계열을 정상성을 나타내도록 만드는 한 가지 방법으로 연이은 관측값의 차이를 계산하여 데이터가 정상성을 나타내도록 변화시킵니다.
lag(시차)? 특정 활동이 데이터의 변화에 영향을 준 시간
- 원유 관련 뉴스가 원유 가격에 영향을 주는 시간이 1일이었으면 시차는 1일

시계열 통합, 합집합, 역차분, 부분추출, 수정 등을 할 수 있음

위의 그림은 로그 변환, 1차 차분, 2차 차분 수행 결과를 시각화한 결과입니다. 일반적으로 시계열 곡선이 특정한 트렌드를 가지고 있다면 1차 차분을, 시간에 따라 변화하는 트렌드가 있다면 2차 차분을 수행합니다.(링크)

Ch 5. 시계열 데이터의 EDA

Exploratory Data Analysis (탐색적 데이터 분석)
상태 공간 모형을 사용한다는 것은 기존의 예측 문제와 더불어 현재 혹은 상태 변수 값을 추정하는 것을 목표로 한다는 것을 의미한다
- 상태공간 모형(State-Space Model): Markov chain을 기반으로 하는 시계열 모형의 일종이지만, 실제 관측가능한 observation 데이터와 hidden state data가 결합하여 만들어진다.
- $Y_j = \{y_1, y_2, ... , y_j\} \to [\text{State Space Model}] \to x_t$ 추정
- j < t -> Prediction
- j = t -> Filter
- j > t -> Smoothing
대표적으로 필터링(filtering) 문제와 스무딩(smoothing) 문제가 있다.

상태 공간 모형... 뭔가 있어보이는데 그냥 간단히 생각해보면 관측 할 수 없거나 어려운 변수에 대해서 예측하는 모델을 따로 두고 얘를 같이 활용해서 조금 더 정확한 예측을 해보자.. 인 듯한 느낌

평활화(Smoothing)

평활화(smoothing) 문제는 현재까지 수집한 관측치 y1,⋯,yt 를 이용해서 현재까지의 상태 변수 히스토리 x1,⋯,xt 을 전체를 모두 재추정하는 문제를 말한다. 금융 분야에서 팩터 모형(factor model)의 계수를 추정하는 문제도 스무딩 문제에 속한다. 또한 시계열 자료 중 누락된 자료(missing data)가 있는 경우에도 스무딩 문제 해결을 통해 누락된 자료를 추정할 수 있다.
시계열 자료에서 무작위성을 줄이는 기법
평활화 개념에 Filter 를 포함하기도 함

이동평균 평활법(Moving Average, MA Smoothing)
지수 평활법(Exponential Smoothing): 단순 지수평활, 이중 지수평활
OLS Smoothing (회귀모형 평활법)
Holt-Winters Smoothing
Kernel Smoothing

이동 평균법

필터링(Filtering)

필터링(filtering) 문제는 현재까지 수집한 관측치 y1,⋯,yt 를 이용해서 현재의 상태 변수 값 xt 을 추정하는 문제이다. 칼만 필터는 컴퓨터 비전, 로봇 공학, 레이다 등의 여러 분야에 사용된다. 칼만 필터는 과거에 수행한 측정값을 바탕으로 현재의 상태 변수의 결합분포를 추정한다.

이동평균 평활법 분석사례: filter (4가지 방법)

1. 단순 이동평균 평활법(Simple Moving Average Smoothing)

H0: 각 값은 독립이며 자기 상관이 없다

( ff <- filter(dd1.ts, filter=rep(1, 4)/4, method="convolution", sides=1) ) # 평활상수 filter = 0.25 (m=4) 앞뒤로 얼마나 볼 것이냐
plot(dd1.ts, main="Simple Moving Average Smoothing: dd1")
lines(ff, col="red", lty=2, lwd=2) # fitted line 진한 빨강 점선으로
abline(h=mean(dd1.ts), col="red")

box test 결과, X-squared = 0.68668, df = 1, p-value = 0.4073
P 값이 높으므로 H0 기각(H0라는 사건이 우연히 일어날리가 없다)

2. 이중 이동평균 평활법(Double Moving Average Smoothing)

( ff1 <- filter(dd1.ts, filter=rep(1, 3)/3, method="convolution", sides=1) ) # 평활상수 filter= 0.33 (m=3) #1번째
( ff2 <- filter(ff1, filter=rep(1, 3)/3, method="convolution", sides=1) ) # 평활상수 filter= 0.33 (m=3) #2번째

MV를 구한다음 그걸로 다시 MV를 또 구한다
조금 더 스무스한 선이 그려짐

Box-test 결과 : X-squared = 0.737, df = 1, p-value = 0.3906 (조금 줄어들음)

3. 가중 이동평균 평활법

w1 <- c(0.4, 0.3, 0.2, 0.1) # 평활상수 filter = (0.4, 0.3, 0.2, 0.1) # 동일 가중이 아니라
(ff3 <- filter(dd1.ts, filter=w1, method="convolution", sides=1)) # 직전 시간에 40%, 그 이전 30% 등 차별 가중

조금 더 실제 값에 가까운 선이 그려짐

X-squared = 1.2749, df = 1, p-value = 0.2588
tsdisplay(res, main="Residuals by Moving Average: dd1")

4. 이중 가중 이동평균 평활법(Double Weight Moving Average Smoothing)

w1 <- c(0.4, 0.3, 0.2, 0.1)
ff3 <- filter(dd1.ts, filter=w1, method="convolution", sides=1)
( ff4 <- filter(ff3, filter=w1, method="convolution", sides=1))

X-squared = 0.93339, df = 1, p-value = 0.334

스무드 해졌으나 잔차는 여전히 크다
각 방식 별 Forecast 결과

f1 <- forecast(ff, h=1)
f2 <- forecast(ff2, h=1)
f3 <- forecast(ff3, h=1)
f4 <- forecast(ff4, h=1)
print(f1)
print(f2)
print(f3)
print(f4)

#       	Point Forecast    Lo 80    Hi 80    Lo 95   Hi 95
#2021 Q1       1330.823 1295.575 1366.071 1276.916 1384.73
#				Point Forecast    Lo 80    Hi 80   Lo 95    Hi 95
#2021 Q1       1331.444 1306.824 1356.065 1293.79 1369.098
#				Point Forecast    Lo 80    Hi 80    Lo 95    Hi 95
#2021 Q1       1329.126 1285.268 1372.984 1262.051 1396.201
#				Point Forecast    Lo 80    Hi 80    Lo 95    Hi 95
#2021 Q1       1333.871 1312.34 1355.403 1300.942 1366.801

요소분해(Decomposition)

시계열 자료는 우연변동, 추세변동, 계절변동, 주기변동 등 다양한 변동의 성분이 중첩되어 있다.
시계열 자료에서 추세 및 주기의 유무와 크기를 파악하는 일은 시계열 분석에서 중요한 EDA의 하나이며, 대표적인 방법이 요소분해법(Decomposition)이다.
시계열 자료를 우연변동, 추세변동, 주기변동으로 구분하여 이를 각 요소로 분해하게 되는데, 분해방법에 따라
- 선형적으로 구성되는 가법모형(Additive)과
- 비선형적으로 구성되는 승법모형(Muliplicative)으로 구분된다.
- 가법 모형
  $$y_t=T_t+S_t+I_t$$
  - $y_t$: t시점에서의 관측값
  - $T_t$: t시점에서의 추세효과에 의한 기여분
  - $S_t$: t시점에서의 계절효과에 의한 기여
  - $C_t$:일반적으로 순환성은 장기간에서만 고려되기 때문에 0
- 승법 모델

중첩된 변동요인을 분해하는 목적은 시계열 자료에서 추세변동과 주기변동을 제거할 경우 남은 잔차(Residual) 시계열 자료를 우연변동에 의한 정상 시계열(Stationary Time Series)로 만들 수 있기 때문이다.
- 시계열 자료의 대부분은 추세변동과 주기변동을 제외할 경우 잔차 시계열은 정상 시계열이 된다.
- 잔차가 정상 시계열이 되지 않는 경우 보다 정밀한 추가 분석이 필요할 수도 있다.
- 정상성(Stationary)?
  - 시간에 상관없이 일정한 성질을 띠고 있는 것
  - ‘약 정상성을 띠는 시계열 데이터는 어느 시점(t)에 관측해도 확률 과정의 성질(E(Xt), Var(Xt))이 변하지 않는다’
시계열 성분 추출은 decompose를 이용하며 가법모형과 승법모형으로 구분한다.
- 가법 모형 예시

계절 변동을 제거한 시계열 자료

ddd1 <- dd4 - dd4_a$seasonal # 계절변동 제거자료 # 1320.852-178.852 = 1142
plot(ddd1, main="Decomposition of Seasonal Variation: ddd1") # 추세변동을 제거한 시계열 자료

추세 변동을 제거한 자료

ddd2 <- dd4 - dd4_a$trend # 추세변동 제거자료
plot(ddd2, main="Decomposition of Trend Variation : ddd2") # 추세변동을 제거한 시계열 자료

시계열 자료 $y_t$를 추세 및 주기변동(TC), 계절변동(S), 우연변동 (I) 등으로 구분하여 성분을 추출한다.
승법모형은 Log 변환으로 가법모형이 된다.
- 가법모형: $y_t = TC_t + S_t + I_t$
- 승법모형: $y_t = TC_t * S_t * I_t$
- 일반적으로 가법모형보다는 승법모형이 현실적이다. 가법모형은 다른 변동들이 어느정도인지에 상관없이 특정 변동이 일정하게 시계열자료(Yt)에 영향을 준다는 것이 전제가 되어 있는 반해, 승법모형은 특정변동이 Yt에 미치는 영향은 다른 변동들의 값에 따라 달라진다는 것을 반영한다는 모형이다. 따라서 대부분의 시계열자료는 승법모형으로 간주되며 분해법의 승법모형으로 요소를 분해하는 것이 일반적이다.

시계열 상관관계(Serial Correlation)

spurious correlation: 허위 상관, 통계적으로는 관련이 있어 보이지만 실제 인과관계는 없는 상황
omitted variable bias:

Ch 6. 요약

시계열 데이터란?

시계열은 동일한 대상을 다른 시점에 걸쳐 관측한 일련의 기록이다. 시계열 분석을 따로 할애해서 학습해야 하는 이유는 시계열 데이터의 통계적 특성 때문이다. 일반적인 인과 추론 문제에서 가정하는 i.i.d. (개별 데이터간 독립성)를 만족시키지 않고, 관측 데이터 포인트간 자기상관성(autocorrelation)을 보이기 때문이다.
시계열에서 자기상관이란 특정 시점(t) 관측치가 이전 시점(t-1, t-2, …, t-k) 관측치와 상관관계가 있다는 뜻이며, 현재 데이터가 과거 시점 데이터에 의해 얼마나 영향을 받는지를 기억(memory)으로 표현한다. 딥러닝을 이용한 시계열 모형의 대표주자인 LSTM(Long Short-term Memory, 장단기 기억모형)의 M이 Memory에서 왔다는 점을 상기하면 쉬울 것이다. 즉, 시계열 모델링의 기본은 현재 데이터를 설명하는 데에 있어 과거 시점의 데이터가 얼마나 쓰이는지에 따라 달라진다고 할 수 있다.

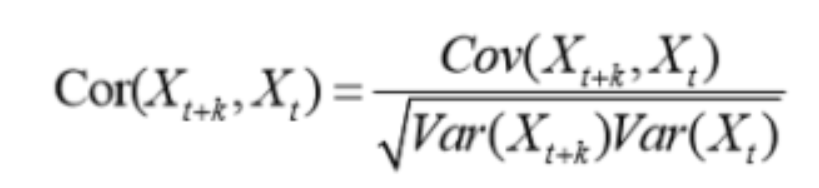
마르코프 성질하고는 어떤 관계가 있을까?
넓게 보자면 금융시계열 뿐 아니라 센서데이터, 제조데이터, 기상데이터 등도 시계열 데이터라 할 수 있으며, 각자의 특성에 맞게 발전해온 분석모델이 있다. 보통 시계열 데이터의 분석방법론은 시간 영역(time domain)과 진동수 영역(frequency domain)으로 나뉜다. 예를 들어 신호 처리(signal processing) 분야에서는 진동수를 주된 분석대상으로 하고 있어, 방법론적인 주된 관심사는 푸리에 변환(Fourier transform) 등을 통하여 진동수의 노이즈를 제거하는 방법이 되고 있다.
반면 우리가 대체로 이해하는 시계열 데이터는 일정한(fixed) 이산적인(discrete) 시간 간격을 가지는 것을 전제로 하며, 실무에서도 time domain의 방법론을 이용하는 것이 주가 된다. 이러한 계열(series) 개념은 확장되어 전산언어학에서는 문장을 하나의 연속된 배열(sequence)로 보았고, 자연어 분석(NLP)에서 시계열 딥러닝의 큰 도움을 받았다. 자연어 분석에의 응용 예제는 Part 6.에서 다루게 될 것이다.

'인공지능 > [강의] 딥러닝, 머신러닝을 활용한 시계열 데이터 분석' 카테고리의 다른 글

AR, MA, ARMA, ARIMA 관련 기본 설명, 비트코인 예시 링크 (0)	2024.11.13
[강의 요약] 패캠 시계열 분석 - Part5. 딥러닝을 이용하여 정교하게 예측하기 (0)	2024.11.13
[강의 요약] 패캠 시계열 분석 - Part4. 다변량 시계열 (0)	2024.11.13
[강의 요약] 패캠 시계열 분석 - Part3. 본격 시계열 분석하기 (0)	2024.11.13
[강의 요약] 패캠 시계열 분석 - Part2. 머신러닝으로 데이터 실무 맛보기 (0)	2024.11.13