Ch 2. 데이터 수집하기
자본시장 시계열 소개
1. 가격 시계열 vs 수익률 시계열
- scale-free
- stationary (<- random walk)
- 금융시장에서는 거의 정상 시계열이 없다
- distributional advantages
2. 수익률의 측정
- (t-1 ~ t 기간 동안의) (One-period) Simple Return
- (t-1 ~ t - k 기간 동안의) (Multiperiod) Simple Return
- One-period Simple Return
$$1+R_t=\frac{P_t}{P_{t-1}}$$
$$P_t=P_{t-1}(1+R_t)$$
- Multiperiod Simple Return

3. 연속복리 수익률(Continously Compounded Return)
- 로그 수익률
- 퍼센트 수익률 \(r_t = 100 * \ln (P_t / P_{t-1})\)
- Continuously Compounded Return

자본시장 시계열(수익률 분포)의 주요 통계적 속성
1. 일별 수익률 분포의 통계적 특성
- (참고) 선행개념: 확률밀도함수(Probability Density Function, pdf)
- 왜도(skewness)가 높다
- 비대칭성
- 정의: (확률밀도함수의 3rd central moment)
- 첨도(kurtosis)가 높다
- 두꺼운 꼬리분포(fat-tail)
- 정의: (확률밀도함수의 4th central moment)
- 정규분포의 경우 K(x) = 3이며, K(x) - 3 > 0 인 경우 첨도가 높다고 본다
- 실무적으로는 정규분포에 비하여 극단값(extreme value)를 가질 확률이 높다는 뜻(leptokurtic)
- 반대로 K(x) - 3 < 0 인 경우는 short-tail로 볼 수 있으며 극단적인 경우 uniform distribution over a finite interval 이 됨 (platykurtic)
- (일별, 월별, 연별) 수익률의 시계열적 특징: 자기 상관성이 없다(가격이랑 다름)
- 금융시장이 그만큼 Random Walk 하게 움직인다는 뜻

2. (c.f.) 자산 수익률을 측정하는 다른 방법
- APR (Annual Percentage Rate), CAGR (Compound Annual Growth Rate)

data.pct_change().mean().plot(kind='bar', figsize=(10, 6))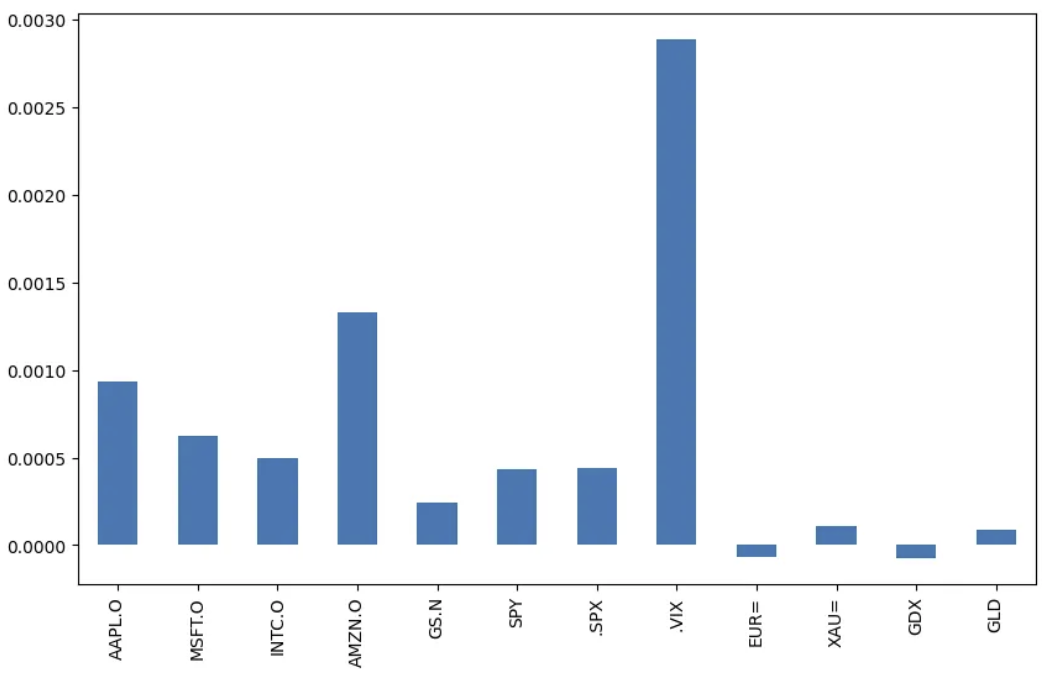
Ch 3. 금융시계열 이용하여 시장 예측하기
시계열을 금융분석에 응용하기

변동성의 개념과 모형의 필요성
- 금융시계열에서 수익률의 분산을 보는 이유
- t시점의 수익률 = \(100 * \ln(x_t / x_{t-1})\)
- 시간가변하는 변동성을 모형화하는 경우, 분산이 시점 t에 의존하므로, t-1기까지의 정보를 이용하여 변동성을 측정하는 조건부 분산이 예측오차를 줄일 수 있다는 장점을 가진다
- 지금까지 다룬 시계열 분석은 다른 변수 또는 해당 변수 자체의 과거값의 변화에 대응하는 종속변수의 평균적인 변화 분석에 초점을 둠
- 따라서 회귀모형 또는 시계열 모형에 포함되는 오차항에 대한 정보는 추정값에 대한 통계적 추론을 위하여 보조적 역할이었음
- 금융시장의 변동성은 시간에 따라 변화하는 것이 일반적
- 변동성이 커진다는 것은 일반적으로 자산시장으로 유입되는 정보의 양이 많아짐을 뜻함
- 예) FOMC 금리 발표, 신흥국 환 위기, 유럽발 재정위기, 산유국 감산 소식 등
- 금융시장에서 변동성에 대한 관심이 증가함에 따라 금융시계열의 분산(variance) 및 공분산(covariance) 등에 대한 추정과 예측이 필요
- 변동성
- 변동성은 자산 수익의 표준편차 혹은 분산으로 측정됨
- 대부분의 금융시계열은 변동성의 군집현상(volatility clustering)이 나타남
- 오차항의 분산이 일정하다는 OLS 회귀모형의 기본 가정을 위배
- 기준금리를 비롯한 각종 경제지표의 발표, 금융위기, 재정 위기와 같은 외부 충격(shock)에 영향을 받는다는 의미
- 이러한 충격이 일정기간 동안 영향을 미치게 되므로 시계열상 이분산성이 발생
- 조건부 분산
- x 의 값을 알고 있을 때 이에 대한 조건부확률분포 p(y|x)의 분산
- 예측문제의 관점으로 보면 조건부분산은 예측의 불확실성를 뜻함
- 조건부 이분산성 (Conditional Heteoskedasticity)
- 오차항의 분산과 독립변수가 일정한 관계를 가질 수 있다
변동성 모형: ARCH, GARCH
ARCH (AutoRegressive Conditional Heteroskedasticity)
- ARCH 는 Engle(1982)에 의해 제시되었으며, 오차항의 분산의 현재값이 이전의 오차항의 제곱값들에 의존할 것이라는 접근에서 출발
- "바로 직전의 오차항의 제곱값에 의존": \(σ_t^2 = α_0 + α_1 * ϵ_{t-1}^2\)
- 전체 모형은 조건부 평균과 분산에 대해 두 개의 구별되는 모형을 포함함
- ARCH 모형의 문제점
- 양(+)의 shock과 음(-)의 shock을 동일하게 다루고 있음(과거 shock의 제곱값)
- : 실제로는 방향에 따라 비대칭적인 영향력을 보일 때가 많다
- ARCH 의 차수를 어떻게 결정해야 하는가?
- : 실제로 필요한 q 값이 상당히 클 수가 있음
- 조건부 분산이 양(+)이 되기 위한 충분조건은 파라미터가 모두 비음성(non-negative)이어야 함
- : 추정해야하는 모수가 많아지는 경우 이러한 제약이 충족되지 않을 수 있음
GARCH (Generalized AutoRegressive Conditional Heteroskedasticity)
- ARCH 모형과 달리, GARCH 모형은 변동성의 시계열 의존성, 즉 자기상관을 표현하는 데 있어서 모수의 수를 줄일 수 있다는 장점
- GARCH 모형은 조건부분산이 직전의 오차항의 제곱값과 함께 자체 시차값(lagged values)에 의존하도록 함
- GARCH (1,1)
- (1) \(Y_t = γ_0 + γ_1* X_{1t} + ... + γ_k*X_{kt} + ϵ_t\)
- (2) \(σ_t^2 = ω + α_0 + α_1 * ϵ_{t-1}^2 + ... + α_q * ϵ_{t-q}^2\)
- 조건부 평균에 대한 식 (1) 은 외생 변수 및 오차항의 함수로 표현됨
- GARCH(1, 1) = ARCH(∞) 모형이므로 추정해야 하는 모수의 수를 줄일 수 있다는 장점
벡터자기회귀(Vector AutoRegressive Model, VAR)
- 실증분석에서는 2개 이상의 시계열을 동시에 모형화하는 것이 유리
- 자산시장를 비롯한 거시경제 시계열은 서로 독립적으로 움직이는 것이 아니라 일정한 상관관계를 보이는 편
- 벡터자기회귀(VAR)은 k개의 AR식을 벡터로 쌓은 것과 같다
- 다만 단일 시계열 AR과 다른 점은 설명변수로 자기 자신의 lag뿐 아니라 다른 변수들의 lag도 포함한다는 점
벡터오차수정모형(Vector Autocorection Model, VECM)
- 공적분 관계의 존재 여부에 따라 VAR와 VECM을 선택
- 공적분(Cointegration): 두 비정상 시계열을 선형조합 했을 때 시계열의 적분 차수가 낮아지거나 정상상태가 되는 경우
- 적분차수: 정상성이 되기까지 차분해야 하는 횟수
- 두 개 이상의 시계열이 공적분 관계에 있으면 장기관계 또는 균형관계를 가진다는 의미
- VAR 모형은 각 시계열이 안정성 조건을 만족하지 않아도 사용할 수 있지만, 일반적으로 불안정성 시계열의 경우 차분을 하거나 변수간 장기적 관계에 대하여 정보를 상실할 수 있다는 단점
- 따라서 변수간 공적분 관계에 있는 시계열은 차분을 거치지 않고 원 데이터를 써서 모형에 적합시킬 수 있다는 점에서 장점을 가진다
- "Spurious Correlation" (가짜 상관관계)
충격반응함수 (Impulse Response Function, IRF)
- 충격반응함수는 VAR의 추정계수를 바탕으로 모형 내 변수에 대하여 일정한 크기의 충격을 가할 때 모형의 모든 변수들이 시간의 흐름에 따라 어떻게 반응하는가를 나타낸 것
- 내생변수의 현재값과 미래값에 대한 오차항 중 하나에 대한 1표준편차 충격(one standard deviation shock)의 효과를 추적함
- 즉, 특정 변수의 단위당 충격(unit shock)의 크기에 해당하는 충격을 그것이 자기 자신의 변수와 나머지 변수에 미치는 영향을 의미
- 변수간의 상호인과관계를 분석하고 변수의 변화에 따른 파급효과를 분석하는 데 이용
'인공지능 > [강의] 딥러닝, 머신러닝을 활용한 시계열 데이터 분석' 카테고리의 다른 글
| AR, MA, ARMA, ARIMA 관련 기본 설명, 비트코인 예시 링크 (0) | 2024.11.13 |
|---|---|
| [강의 요약] 패캠 시계열 분석 - Part5. 딥러닝을 이용하여 정교하게 예측하기 (0) | 2024.11.13 |
| [강의 요약] 패캠 시계열 분석 - Part3. 본격 시계열 분석하기 (0) | 2024.11.13 |
| [강의 요약] 패캠 시계열 분석 - Part2. 머신러닝으로 데이터 실무 맛보기 (0) | 2024.11.13 |
| [강의 요약] 패캠 시계열 분석 - Part1. 데이터 분석 첫 걸음 떼기 (0) | 2024.11.12 |

