이전까지 배운 Q 러닝, SARSA, 몬테카를로 법 등은 크게 보면 가치 기반(value-based method)로 분류된다. 여기서 말하는 '가치'는 행동 가치 함수(Q 함수)나 상태 가치 함수(V)를 뜻한다. 가치 기반 기법은 가치 함수를 모델링하고 가치 함수를 학습한다. 그리고 가치 함수를 경유하여 정책을 얻는다.
이번 장에서는 가치 기반 기법과는 다른 '정책 경사법(Policy Gradient)'에 의한 알고리즘에 대해서 알아보고자 한다.
가장 간단한 정책 경사법
정책 경사법은 경사, 즉 기울기(gradient)를 이용하여 정책을 갱신하는 기법들의 총칭이다. 가장 간단한 알고리즘부터 살펴보자.
정책 경사법 도출
이번 장에서는 정책을 신경망 모델로 표현한다. 신경망의 매개변수 전체를 \(\theta\)로 표현하면 신경망으로 구현한 정책은 \(\pi_\theta(a|s)\)가 된다.
이제 이 정책 \(\pi_\theta\)를 이용하여 목적 함수를 설정하고, 신경망 학습을 통해 이 목적 함수의 값을 가장 크게 만드는 \(\theta\)를 찾아서 최적화 해야 한다. 일반적인 최적화 문제에서는 목적 함수 대신 손실함수를 설정하여 경사 하강법을 통해 최소값을 찾지만 여기서는 목적 함수를 찾고 경사 상승법을 통해 최대값을 찾는다.
이제 \(\pi_\theta\)를 사용하여 목적 함수를 설정해보자. 일회성 과제이고 정책 \(\pi_\theta\)에 따라 다음 시계열 데이터를 얻었다고 하자.
$$\tau = (S_0, A_0, R_0, S_1, A_1, R_1, \cdots, S_{T+1})$$
\(\tau\)는 궤적(trajectory)를 의미한다. 이때 수익은 다음과 같이 표현할 수 있다.
$$G(\tau) = R_0 + \gamma R_1 + \gamma^2 R_2 + \cdots + \gamma^T R_T$$
그러면 목적 함수는 다음처럼 표현된다.
$$J(\theta) = \mathbb{E}_{\tau \text{~} \pi_\theta}[G(\tau)]$$
수익 \(G(\tau)\)는 확률적으로 변하기 때문에 그 기대값이 목적 함수가 된다.
목적 함수가 정해지면 다음으로 \(\theta\)에 대한 기울기\(\nabla_\theta\)를 구해야 한다.
정책 \(\pi_\theta\)에 따라 궤적 \(\tau\)를 얻을 수 있는 확률을 \(Pr(\tau|\theta\))로 표현하면 \(\nabla_\theta J(\theta)\)는 다음처럼 전개 가능하다.

위에서 '로그-기울기 트릭'이란 로그의 미분법에 의해 다음이 성립함을 의미한다.
$$\nabla_\theta \log Pr(\tau|\theta) = \frac{\nabla_\theta Pr(\tau|\theta)}{ Pr(\tau|\theta)}$$
이어서 식 D.1을 더욱 확장하기 위해 다음 관계를 이용한다.
$$\begin{equation} \begin{split} Pr(\tau|\theta)&=p(S_0)\pi_\theta(A_0|S_0) p(S_1|S_0, A_0) \cdots \pi_\theta(A_T|S_{T}) p(S_{T+1}| S_{T}, A_T) \\ &= p(S_0) \prod_{t=0}^T \pi_\theta(A_t|S_t) p(S_{t+1}|A_t, S_t) \end{split} \end{equation}$$
\(p(S_0)\)는 초기 상태가 \(S_0\)일 확률이다. 이 식과 같이 궤적 \(\tau\)를 얻을 확률은 초기 확률, 정책, 상태 전이 확률의 곱으로 표현되므로 \(\log Pr(\tau|\theta)\)는 다음과 같이 표현된다.
$$\log Pr(\tau|\theta) = \log p(S_0) + \sum_{t=0}^T \log p(S_{t+1}|S_t, A_t) + \sum_{t=0}^T \log \pi_\theta(A_t|S_t)$$
이제 이 식으로부터 \(\nabla_\theta \log Pr(\tau|\theta)\)는 다음과 같이 구할 수 있다.
$$ \begin{equation} \begin{split} \nabla_\theta \log Pr(\tau|\theta) &= \nabla_\theta \{ \log p(S_0) + \sum_{t=0}^T \log p(S_{t+1}|S_t, A_t) + \sum_{t=0}^T \log \pi_\theta(A_t|S_t) \} \\ &= \nabla_\theta \sum_{t=0}^T \log \pi_\theta(A_t|S_t) \end{split} \end{equation} $$
(\(\nabla_\theta\)는 \(\(theta\)\)에 대한 기울기이므로 관련 없는 항을 모두 지울 수 있음)
따라서 최종적으로 정리하면,
$$ \begin{equation} \begin{split} \nabla_\theta J(\theta) &= \mathbb{E}_{\tau \text{~} \pi_\theta} [G(\tau) \nabla_\theta \log Pr(\tau|\theta)] \\ &= \mathbb{E}_{\tau \text{~}\pi_\theta} \Big[ \sum_{t=0}^T G(\tau) \nabla_\theta \log \pi_\theta(A_t|S_t) \Big] \end{split} \end{equation} $$ (식 9.1)
이 식에서 주목할 점은 \(\nabla_\theta\)가 \(\mathbb{E}\)안에 들어있다는 점인데(기울기 계산은 \(\nabla_\theta \log \pi_\theta(A_t|S_t)\)로 이루어진다), 이 기대값은 몬테카를로법으로 구할 수 있다.
\(\nabla_\theta J(\theta)\)가 구해지면 경사 상승법에 의해 다음처럼 \(\theta\)를 갱신한다.
$$\theta \gest \theta + \alpha \nabla_\theta J(\theta)$$
이 식과 같이 \(\theta\)를 알파만큼 기울기 방향으로 갱신한다.
정책 경사법 알고리즘
\(\nabla_\theta J(\theta)\)는 [식 9.1]과 같이 기대값으로 표현되기 때문에 몬테카를로법을 통해 샘플링을 여러 번 하여 평균을 구하여 계산해야 한다. 이번 장에서는 간단히 에피소드 샘플 수가 1개인 경우를 생각해보자.
$$\nabla_\theta J(\theta) \simeq \sum_{t=0}^T G(\tau) \nabla_\theta \log \pi_\theta(A_t|S_t)$$
위 식은 \(\nabla_\theta \log \pi_\theta(A_t|S_t)\)를 모든 시간(t=0~T)에서 구하고, 각 기울기에 수익 \(G(\tau)\)를 '가중치'로 곱하여 모두 더한 것으로 해석 할 수 있다.

위 그림에서 수행하는 계산의 '의미'를 생각해보자. 우선 log 미분으로 다음의 식이 성립한다.
$$\nabla_\theta \log \pi_\theta (A_t|S_t) = \frac{\nabla_\theta \pi_\theta (A_t|S_t)}{\pi_\theta(A_t|S_t)}$$
이 식과 같이 \(\nabla_\theta \log \pi_\theta(A_t|S_t)\)는 \(\nabla_\theta \pi_\theta(A_t|S_t)\)라는 기울기(벡터)에 \(\frac{1}{\pi_\theta(A_t|S_t)}\)을 곱한 것이다. \(\nabla_\theta \pi_\theta(A_t|S_t)\)가 가리키는 방향은 상태 \(S_t\)에서 \(A_t\)를 취할 확률이 가장 높아지는 방향을 가리킨다. 그리고 그 방향에 대해 \(G(\tau)\)라는 '가중치'가 곱해진다.
(Q. 직전의 행동 \(A_t\)에 대해서 수익이라는 가중치를 통해 학습이 되는데 가중치가 모두 양수인 게임에서는 학습이 잘 안되지 않을까?)
정책 경사법 구현


update() 메소드는 에이전트가 목표에 도달했을 때 호출된다. 먼저 수익 G를 계산하고 각 스텝에서 취한 행동에 대한 확률 prob을 통해서 -F.log(prob)을 구하고, 가중치 G를 곱한 뒤 모두 더하여 손실 함수를 계산한다.

실험 결과를 보면 점차 나아지고 있으나 아직 개선의 여지가 많아 보인다.
REINFORCE
REINFORCE는 앞 절의 정책 경사법을 개선한 기법이다.
(REINFORCE: REward Increment = Nonenegative Factor X Offset Reinforcement X Charactertistic Eligibility)
REINFORCE 알고리즘
앞에서 살펴본 가장 간단한 정책 경사법은 다음과 같았다.
$$ \begin{equation} \begin{split} \nabla_\theta J(\theta) &= \mathbb{E}_{\tau \text{~}\pi_\theta} \Big[ \sum_{t=0}^T G(\tau) \nabla_\theta \log \pi_\theta(A_t|S_t) \Big] \end{split} \end{equation} $$ (식 9.1)
여기서 \(G(\tau)\)는 지금까지 얻은 모든 보상의 할인율이 적용된 합이다. \(G(\tau) \nabla_\theta \log \pi_\theta(A_t|S_t)\)를 보면 특정 시간 t에서 행동 \(A_t\)를 할 확률에 '항상 일정한 가중치 \(G(\tau)\)'가 곱해진다.
그런데 어떤 행동이 좋은지 나쁜지는 사실 행동 이후에 얻은 보상의 총합으로 평가된다. 그 행동 이전에 얻은 보상에 대해서는 무관하다고 보는 것이 맞다.
따라서 식 9.1에서 행동 \(A_t\)에 대한 가중치 \(G(\tau)\)에는 본질적으로 관련이 없는 보상이 노이즈로 섞여 있다는 뜻이다. 이 노이즈를 제거하기 위해 가중치 \(G(\tau)\)를 다음과 같이 변경할 수 있다.
$$ \begin{equation} \begin{split} \nabla_\theta J(\theta) &= \mathbb{E}_{\tau\text{~}\pi_\theta} \Big[ \sum_{t=0}^T G_t \nabla_\theta \log \pi_\theta(A_t|S_t) \Big] \end{split} \end{equation}$$
$$G_t = R_t + \gamma R_{t+1} + \cdots + \gamma^{T-t}R_t$$
변경된 가중치 \(G_t\)는 t~T 시간 동안에 얻은 보상의 총합이다. 즉, t 시간 이전에 얻은 보상은 포함하지 않는 가중치를 통해서 \(A_t\)를 강화하는 것이다.
위 식에 기반한 알고리즘을 REINFORCE라고 한다. 앞서 나온 식 9.1과 위 식 모두 샘플 수를 무한히 늘리면 정확한 \(\nabla_\theta J(\theta)\)에 수렴한다. 반면 샘플이 흩어진 정도인 '분산'은 식 9.1이 더 크다. 앞서 말한 것처럼 관련 없는 노이즈가 섞여 있기 때문이다.
REINFORCE 구현

앞서 구현한 코드와 다른 점은 update() 메서드에서 각 시각의 G를 계산하여 손실 함수를 갱신한다는 점이 다를 뿐이다.

실험 결과를 봐도 앞 절의 결과보다 훨씬 안정적이고 빠르게 학습됨을 볼 수 있다.
베이스라인
이제 REINFROCE를 개선할 수 있는 베이스라인(baseline) 기술에 대해서 알아보자.
베이스라인 아이디어
A, B, C 세 사람이 시험을 보고 다음의 점수를 얻었다.

이 때 분산은 '466.666..' 이다. 분산은 데이터의 흩어진 정도를 나타내므로 점수의 편차가 심하다는 것이다.
이번에는 세 사람의 평균 점수를 예측값으로 사용하여 차이를 구하고, 그 차이에 대한 분산을 구해보자.

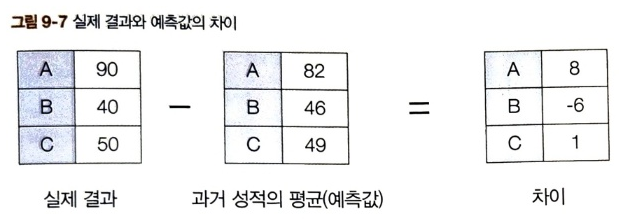
8, -6, 1 세 값의 분산은 32.666... 으로 처음과 비교하면 굉장히 많이 줄어들었다. 이 예에서 알 수 있듯이 어떤 결과에서 예측값을 빼면 분산을 줄일 수 있다. 예측값의 정확도가 높을 수록 분산은 작아진다. 이것이 베이스라인 기법의 아이디어이다. 여기서는 평균을 베이스라인으로 잡았다.
이제 베이스라인을 REINFORCE에 적용해보자.
베이스라인을 적용한 정책 경사법
$$ \begin{equation} \begin{split} \nabla_\theta J(\theta) &= \mathbb{E}_{\tau \text{~} \pi_\theta} \Big[ \sum_{t=0}^T G_t \nabla_\theta \log \pi_\theta(A_t|S_t) \Big] \\ &= \mathbb{E}_{\tau \text{~} \pi_\theta} \Big[ \sum_{t=0}^T (G_t - b(S_t)) \nabla_\theta \log \pi_\theta(A_t|S_t) \Big] \end{split} \end{equation}$$
위 식에서는 \(G_t\) 대신 \(G_t - b(S_t)\)를 사용했다. 여기서 \(b(S_t)\)는 임의의 함수이다. 즉, 입력이 \(S_t\)이기만 하면 어떤 함수라도 상관 없다는 뜻이다. 이 \(b(S_t)\)가 베이스라인이다.
실무에서는 가치 함수(\(V_{\pi_\theta} (S_t)\))를 베이스라인으로 많이 사용한다. 베이스라인을 통해 분산을 줄일 수 있다면 학습 시 샘플 효율이 좋아진다.
참고로 베이스라인으로 가치 함수를 사용하면 실제 가치 함수 \(v_{\pi_\theta}(S_t)\)를 알 수 없다. 이 경우 가치 함수에 대해서도 학습해야 한다.
마지막으로 베이스라인을 사용하는 직관적인 이유를 알아보자. 다음 그림과 같이 OpenAI Gym의 카트폴 게임에서 막대가 균형을 잃어 게임이 끝나기 직전이라고 해보자. 이 상태에서는 어떤 행동을 선택하든 몇 단계 후 게임이 종료된다.

위와 같은 상황에서 어떤 행동을 해도 결국 G를 얻는다면, v(s)도 결국 G이다. 이런 경우, REINFORCE에서는 상태 s에서 어떤 행동 a를 해도 G 만큼 강화가 된다. 하지만 베이스라인을 사용할 경우, G - V(s)만큼 강화가 될 터인데, G-V(s)=0 이므로 어떤 행동이든 그 행동을 선택할 확률이 작아지지도 커지지도 않는다. 이처럼 베이스라인을 사용하면 학습 과정에서의 낭비를 줄일 수 있다.
행위자-비평자(Actor-Critic)
강화 학습 알고리즘은 크게 가치 기반 기법과 정책 기반 기법으로 나뉜다. 이번 장에서 배울 Actor-Critic 알고리즘은 '가치 기반이자 정책 기반' 알고리즘이다.

행위자-비평자 도출
앞서 다룬 '베이스 라인을 적용한 REINFORCE'의 목적 함수 기울기는 다음과 같았다.
$$ \begin{equation} \begin{split} \nabla_\theta J(\theta) = \mathbb{E}_{\tau \text{~} \pi_\theta} \Big[ \sum_{t=0}^T (G_t - b(S_t)) \nabla_\theta \log \pi_\theta(A_t|S_t) \Big] \end{split} \end{equation}$$
이번 장에서는 신경망으로 모델링한 가치 함수를 베이스라인으로 사용하기 위해 다음 기호들을 사용한다.
- \(w\): 가치 함수 신경망의 가중치 매개변수
- \(V_w(S_t)\): 가치 함수를 모델링한 신경망
이제 베이스라인 \(b(S_t)\)를 \( V_w(S_t) \)를 대체해보자. 그러면 목적 함수의 기울기는 다음과 같이 표현된다.
$$ \begin{equation} \begin{split} \nabla_\theta J(\theta) = \mathbb{E}_{\tau \text{~} \pi_\theta} \Big[ \sum_{t=0}^T (G_t - V_w(S_t) ) \nabla_\theta \log \pi_\theta(A_t|S_t) \Big] \end{split} \end{equation}$$ (식 9.5)
하지만 위 식에서 쓰이는 수익 \(G_t\)는 목표에 도달해야 비로소 얻을 수 있기 때문에 단점이 있다. 이 단점을 해결하기 위해 TD법으로 가치 함수를 학습해보자.

위 그림과 같이 가치 함수 학습을 위해 MC에서는 \(G_t\)를 사용하지만 TD에서는 \(R_t+\gamma V_w (S_{t+1})\)을 사용한다.
이제 이 TD 법으로 식 9.5를 다시 써보면,
$$ \begin{equation} \begin{split} \nabla_\theta J(\theta) = \mathbb{E}_{\tau \text{~} \pi_\theta} \Big[ \sum_{t=0}^T ( R_t+\gamma V_w (S_{t+1}) - V_w(S_t) ) \nabla_\theta \log \pi_\theta(A_t|S_t) \Big] \end{split} \end{equation}$$
위 식에 기반한 방법이 행위자-비평자(actor-critic) 기법이다. 여기서 정책 \(\pi_\theta\)는 위 식에 따라 학습시키고 가치 함수 \(V_w\)는 TD 법에 따라 \(R_t+\gamma V_w (S_{t+1})\)에 가까워지도록 학습한다.
Actor-Critic 구현


* v와 pi에 대해서 각각 loss를 따로 구하는 것에 유의
정책 기반 기법의 장점
- 정책을 직접 모델링하기 때문에 효율적
: 우리가 궁극적으로 결국 얻고자 하는 것은 최적 정책이다. 가치 기반 기법은 가치 함수를 추정하고 이를 바탕으로 정책을 결정한다. 반면 정책 기반 기법은 정책을 '직접' 추정한다. 문제에 따라서는 가치 함수의 형태가 복잡한 반면, 최적 정책은 단순할 수 있다. 이런 경우 정책 기반 기법이 더 빠르게 학습하리라 기대 할 수 있다. - 연속적인 행동 공간에서도 사용할 수 있다.
: 만약 행동 공간이 이산적인 상황이 아니라 연속적인 상황이라면 가치 기반 기법을 적용하기 어려워진다.
연속적인 행동 공간의 예시
반면 정책 기반 기법은 연속적인 공간에도 간단하게 대응할 수 있다. 예를 들어 신경망의 출력이 정규분포라고 한다면 신경망은 정규분포의 평균과 분산을 출력할 수 있다. 그 평균과 분산을 바탕으로 샘플링하면 연속적인 값을 얻을 수 있다.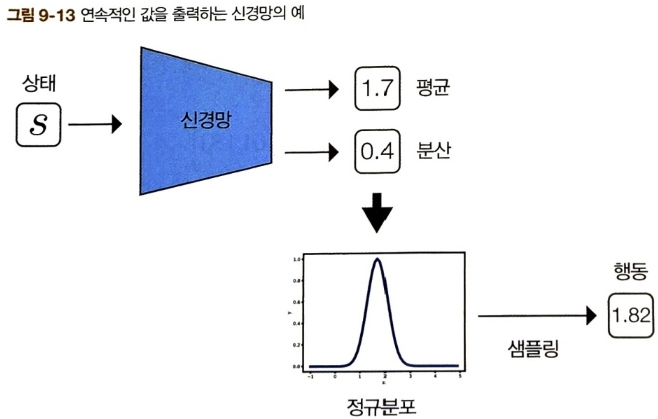
- 행동이 선택될 확률이 부드럽게 변화한다.
:가치 기반 기법에서 에이전트는 Q 함수의 값이 가장 큰 행동을 선택하는데, 이 때 Q 함수가 갱신되면서 값이 최대가 되는 행동이 바뀌면 행동하는 방식도 급격하게 달라진다. 반면 정책 기반 기법에서는 각 행동의 확률이 소프트맥스 함수에 의해 정해지기 때문에 정책의 매개변수를 갱신하는 과정에서 각 행동의 확률이 부드럽게 변화한다. 이 덕분에 정책 경사법의 학습이 안정적으로 이루어 진다.
정리
이번 장에서는 정책 기반 기법인 Policy Gradient에 대해 배웠다.
$$ \begin{equation} \begin{split} \nabla_\theta J(\theta) = \mathbb{E}_{\tau \text{~} \pi_\theta} \Big[ \sum_{t=0}^T \Theta_t \nabla_\theta \log \pi_\theta(A_t|S_t) \Big] \end{split} \end{equation}$$
- \( \Theta_t = G(\tau)\): 가장 간단한 정책 경사법
- \( \Theta_t = G_t\): REINFORCE
- \( \Theta_t = G_t - b(S_t)\): 베이스라인을 적용한 REINFORCE
- \( \Theta_t = R_t + \gamma V_\pi(S_{t+1} - V_pi(S_t)\): Actor-Critic
위 기법들 말고 Q 함수를 사용할 수도 있다.
$$\Theta_t = Q(S_t, A_t)$$
또한 어드밴티지 함수를 사용할 수도 있다.
$$ \Theta_t = Q(S_t, A_t) - V(S_t) = A(S_t, A_t)$$
'인공지능 > [책] 밑바닥부터 시작하는 딥러닝4' 카테고리의 다른 글
| Chapter 10. 한 걸음 더 (0) | 2025.01.19 |
|---|---|
| Chapter 8. DQN (1) | 2025.01.18 |
| Chapter 7. 신경망과 Q 러닝 (0) | 2025.01.17 |
| Chapter 6. TD법(SARSA, Q-learning) (0) | 2025.01.15 |
| Chapter 5. 몬테카를로 법 (0) | 2025.01.14 |

