더 깊게
더 깊은 신경망으로
- 이전 챕터와 달리 아래와 같이 더 깊은 신경망을 사용하면 어떻게 될까?

- 합성곱 계층의 채널 수는 앞 계층에서부터 16, 16, 32, 64 ,64로 늘려간다
- 3x3의 작은 필터를 사용한 합성곱 계층
- ReLU
- 드랍아웃
- Adam
- He 초기화
- 이 모델의 Mnist 결과는 99.38%이다
정확도를 더 높이려면?
- 데이터 확장(Data augmentation)
- 데이터를 회전하거나 이동
- 일부를 잘라내는 crop
- 좌우를 뒤집는 flip
깊게 하는 이유
- 신경망의 매개변수 수가 줄어든다.
- 층을 깊게 한 신경망은 깊지 않은 경우보다 적은 매개변수로 같은 혹은 그 이상의 수준의 표현력을 달성할 수 있다.

- 위와 같은 그림에서, 5X5 = 25개의 매개변수가 필요했던 것이 층을 깊게 하면 3X3 + 3X3 = 18개만 있으면 5X5 크기의 영역에 대한 연산을 할 수 있다.
- 이처럼 작은 필터를 겹쳐 신경망을 깊게 할 때의 장점은 매개변수 수를 줄여 넓은 수용영역(receptive filed)를 소화할 수 있다는데 있다.
- 게다가 층을 거듭하면서 ReLU 등의 활성화 함수를 합성곱 계층 사이에 끼움으로써 신경망의 표현력이 개선된다. 이는 활성화 함수가 신경망에 비선형 힘을 가하고 비선형 함수가 겹치면서 더 복잡한 것도 표현할 수 있게 되기 때문이다.
2. 층을 깊게 함으로써 학습 데이터의 양을 줄여 학습을 고속으로 수행할 수 있다(같은 데이터로도 더 좋은 성능을 낼 수 있다의 의미로 받아들이자)
- 층을 깊게 하면 풀어야 할 문제를 계층적으로 분해하여 더 효율적으로 풀 수 있다. 예를 들어 처음층은 에지 학습에 전념하여 적은 학습 데이터로 효율적으로 학습이 되고, 더 깊은 층은 더 고차원 문제를 해결하는데 집중할 수 있다.
3. 층을 깊게 하면 정보를 계층적으로 전달할 수 있다.
- 예를 들어 에지를 추출한 층의 다음 층은 에지 정보를 쓸 수 있고, 더 고도의 패턴을 효과적으로 학습하리라 기대할 수 있다.
딥러닝의 초기 역사
- 딥러닝이 큰 주목을 받게 된 것은 ILSVRC(ImageNet Large Scale Visual Recognition Challenge) 2012 대회이다.
- 그 해의 대회에서 딥러닝에 기초한 기법, 일명 AlexNet이 압도적인 성적으로 우승하며 이미지 인식에 대한 인식을 뒤흔들었다.
이미지넷
- 이미지넷은 100만장이 넘는 이미지를 담고 있는 데이터셋이다.
- 여러 시험 항목이 있는데 그중 하나가 분류이다.

- AlexNet 이후 딥러닝 모델이 꾸준히 등장하였고 사람의 수준을 넘어섰다.
VGG

- VGG는 합성곱 계층과 풀링 계층으로 구성되는 기본적인 CNN 구조이다. 모두 16층으로 심화한게 특징이다.
- 주목할 점은 3x3의 작은 필터를 사용한 합성곱 계층을 연속적으로 거친다는 것이다.
- 그림에서 보듯 합성곱 계층을 2~4회 연속으로 풀링 계층을 두어 크기를 절반으로 줄이는 처리를 반복한다.
GoogLeNet

- GoogLeNet에는 가로 방향에 ‘폭’이 있다. 이를 인셉션 구조라 한다.

- 인셉션 구조는 크기가 다른 필터(와 풀링)을 여러 개 적용하여 그 결과를 결합한다. 이 인셉션 구조를 하나의 빌딩 블록으로 사용하는 것이 특징이다.
- 또한 1X1 크기의 필터를 사용한 합성곱 계층을 많은 곳에서 사용한다. 1X1 필터는 채널 쪽으로 크기를 줄이는 것으로, 매개변수 제거와 고속 처리에 기여한다.
ResNet
- ResNet(residual network)는 MS에서 개발한 네트워크로 지금까지보다 층을 더 깊게 할 수 있는 특별한 장치를 가지고 있다.
- 딥러닝에서는 층이 지나치게 깊으면 학습이 잘 되지 않고 오히려 성능이 떨어지는 문제가 있었는데 이를 해결하기 위해 스킵 연결(Skip Connection)을 도입했다.

- 입력 신호를 그대로 흘려주기 때문에 역전파 시에 기울기가 작아지거나 지나치게 커질 걱정 없이 앞 층에 ‘의미 있는 기울기’가 전해지리라 기대할 수 있다.

- 위 그림과 같이 ResNet은 합성곱 계층을 2개 층마다 건너뛰면서 층을 깊게 한다. 실험에서는 150층 이상으로 해도 정확도가 오르는 모습이 확인되었다.
더 빠르게(딥러닝 고속화)
- 딥러닝 프레임워크 대부분은 GPU(Graphics Processing Unit)을 활용한다.
- GPU는 병렬 수치 연산을 고속으로 처리할 수 있으니 CNN에서 필요한 단일 곱셈-누산 연산등을 효과적으로 계산할 수 있다.
- GPU는 주로 엔비디아와 AMD 두 회사가 제공한다. 엔비디아는 CUDA, cuDNN 등의 라이브러리를 제공하여 딥러닝에 최적화된 함수를 사요 가능하다.
분산학습
- 딥러닝 계산을 더욱 고속화하고자 다수의 GPU와 기기로 계산을 분산하기도 한다.
- 이 부분에 관해선 책 내용은 너무 옛날 얘기라 딱히 적을 게 없다…
연산 정밀도와 비트 줄이기
- 계산 능력 외에도 메모리 용량과 버스 대역폭 등이 딥러닝 고속화에 병목이 될 수 있다.
- 딥러닝에서는 높은 수치 정밀도(수치를 몇 비트로 표현하느냐)를 요구하지 않는다. 이는 신경망의 견고성에 따른 특징이다.
- 딥러닝은 half-precision(16비트)로도 학습에 문제가 없다는 것이 알려졌다.
딥러닝의 활용
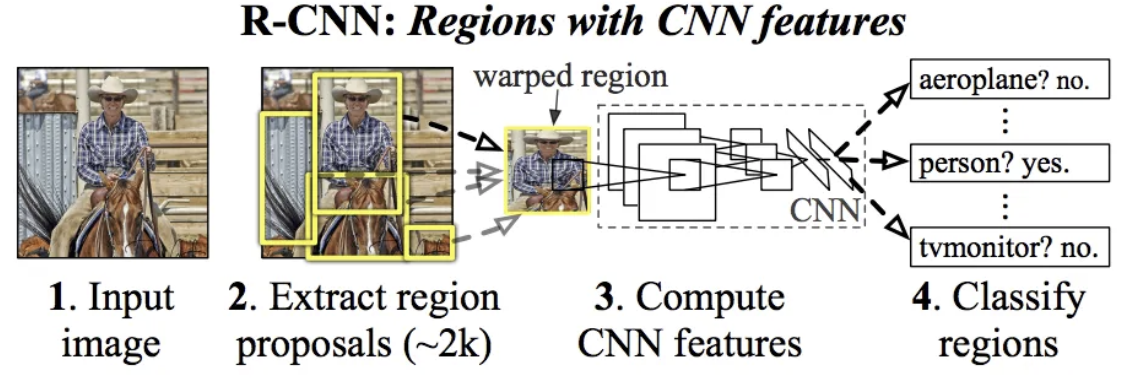
- 이미지 속에 담긴 사물의 위치와 종류(클래스)를 알아내는 ‘사물 검출’
- Faster R-CNN이 대표적
- 분할(Segmentation)
- 분할이란 이미지를 픽셀 수준에서 분류하는 문제이다.
- 아래 그림과 같이 픽셀 단위로 객체마다 채색된 지도 데이터를 사용해서 학습한다. 추론할 때 입력 이미지의 모든 픽셀을 분류한다.

- 이 방법을 구현하는 것의 가장 단순한 방법은 모든 픽셀 각각을 추론하는 것이다.
- 예를 들어 어떤 직사각형 영역의 중심 픽셀의 클래스를 분류하는 신경망을 만들어서, 모든 픽셀을 대상으로 하나씩 추론 작업을 진행한다. 이런 식으로 하면 픽셀의 수만큼 forward 해야하므로 시간이 많이 소요된다.
- 이런 낭비를 줄여주는 기법으로 FCN(Full Convolutional network)가 고안되었다.
- 이는 단 한번의 forward 처리로 모든 픽셀의 클래스를 분류해주는 기법이다.

- 위 그림에서 보듯 FCN에서는 마지막에 공간 크기를 확대하는 처리를 도입했다.
- 이 확대처리로 인해 줄어든 중간 데이터를 입력 이미지와 같은 크기까지 단번에 확대 할 수 있다.
- 이 처리는 이중 선형 보간에 의한 선형확대이다. FCN에서는 이 선형 확대를 역합성곱 연산으로 구현해낸다.
딥러닝의 미래
- 이 책은 너무 옛날에 나온 책이라... 이 책에서 말하는 미래는 도달한지 오래..
- 이미지 스타일 화풍 변환

- 이미지 생성
- 책에서는 DCGAN 등을 소개한다.
- 2024년인 지금은 Diffusion 모델이 대세이다..
자율주행
- SegNet 등으로 주변 환경 인식
Deep Q-Network(강화학습)
- DQN이 적용된 알파고 등..
- 이 책이 나오고 8년이 지난 지금, 밑딥 시리즈 4가 나왔고 메인 주제가 강화학습이다 ㄷㄷ
정리
- 수많은 문제에서 신경망을 더 깊게 하여 성능을 개선할 수 있다.
- 이미지 인식 기술 대회인 ILSVRC에서 최근 딥러닝 기반 기법이 상위권을 독점하고 있다(었다)
- 유명한 신경망으로는 VGG, GoogLeNet, ResNet 등
- GPU와 분산학습, 비트 정밀도 감소 등으로 딥러닝 고속화 가능
- 딥러닝은 사물 인식 뿐 아니라 사물 검출과 분할에도 이용 가능
- 딥러닝의 응용 분야로는 사진의 캡션 생성, 이미지 생성, 강화학습 등이 있다(NLP는 아예 언급도 안하네;; Transformer 나오기 전이라 그런가)
'인공지능 > [책] 밑바닥부터 시작하는 딥러닝1' 카테고리의 다른 글
| [책 요약] 밑바닥부터 시작하는 딥러닝1-Chapter 7. 합성곱 신경망(CNN) (0) | 2024.11.10 |
|---|---|
| [책 요약] 밑바닥부터 시작하는 딥러닝1-Chapter 6. 학습 관련 기술들 (0) | 2024.11.10 |
| [책 요약] 밑바닥부터 시작하는 딥러닝1-Chapter 3. 신경망 (0) | 2024.11.10 |
| [책 요약] 밑바닥부터 시작하는 딥러닝1-Chapter 5. 오차역전파법 (0) | 2024.11.10 |
| [책 요약] 밑바닥부터 시작하는 딥러닝1-Chapter 4. 신경망 학습 (0) | 2024.11.09 |

