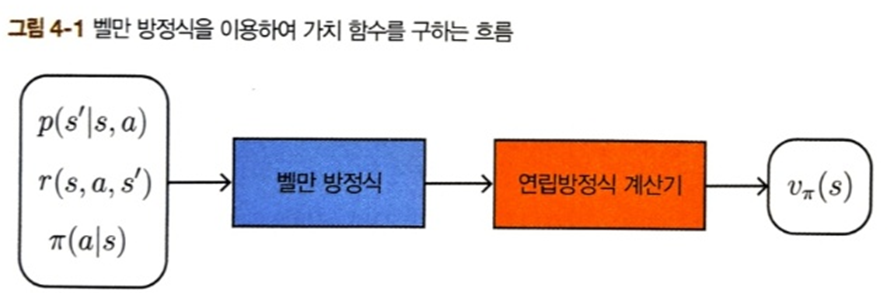
이전 장에서 벨만 방정식에 대해 배웠다. 상태 전이 확률, 보상 함수, 정책이라는 세 가지 정보와 벨만 방정식을 이용하면 가치 함수에 대한 연립 방정식을 얻을 수 있고 이를 풀 수 있다면 가치 함수를 구할 수 있다. 하지만 연립 방정식을 직접 푸는 경우는 간단한 문제에 대해서만 가능하다. 상태와 행동 패턴의 수가 많아지면 감당할 수 없게 된다. 이런 경우에 적용할 수 있는 것이 동적 프로그래밍(Dynamic Programming(DP)) 혹은 동적 계획법이다.
동적 프로그래밍과 정책 평가
동적 프로그래밍을 활용해서 벨만 방정식을 다시 써보자.
기존 벨만 방정식
$$v_\pi(s) = \sum_{a, s'} \pi(a|s) p(s'|s,a) \{r(s,a,s') + \gamma v_\pi(s')\}$$
벨만 방정식은 현재 상태 s의 가치 함수 \(v(s)\)와 다음 상태 s'의 가치 함수 \(v(s')\)의 관계를 나타낸다. 이러한 벨만 방정식을 '갱신식'으로 변형하면 DP 를 사용한 방법이 된다.
$$V_{k+1}(s) = \sum_{a, s'} \pi(a|s) p(s'|s,a) \{r(s,a,s') + \gamma V_{k}(s')\}$$ (4.2)
\(V_{k+1}(s)\)는 k+1 번째로 갱신된 가치 함수를 뜻한다. 이 때의 V(s)는 '추정치' 이기 때문에 실제 가치 함수 v(s)와는 다르다. 그래서 대문자로 표기한다.
이 식의 특징은 다음 상태의 가치 함수 \(V_k(s')\)를 이용하여 '지금 상태의 가치 함수 \(V_{k+1}(s)\)'를 갱신한다는 점이다. 즉, 추정치를 사용하여 추정치를 개선하기 때문에 부트스트래핑(bootstrapping)이라고 부른다.
부트스트랩은 신발(boot)을 신을 때 손가락으로 잡아당기는 신발 뒤쪽에 달려 있는 고리 모양의 끈(strap)을 가리킨다. 여기서 유래하여 다른 사람의 도움 없이 스스로 개선하는 과정을 뜻하는 의미로 쓰이고 있다.
이제 DP를 사용한 구체적인 알고리즘을 설명하겠다. 먼저 \(V_0(s)\)의 초기값을 설정한다. 예를 들어 모든 상태에서 \(V_0(s) =0\)으로 초기화 한다. 그리고 식 4.2를 이용해서 \(V_0(s)\)에서 \(V_1(s)\)을 갱신한다. 이어서 (V_1(s)\)에서 \(V_2(s)\)를 갱신한다. 이 일을 반복하다 보면 최종 목표인 \(V_\pi(s)\)에 가까워진다. 이 알고리즘을 반복적 정책 평가(iterative policy evaluation)이라고 한다. 이 갱신을 반복하면 \(V_\pi(s)\)에 수렴한다는 사실은 이미 증명되었다(sutton, Reinforcement Learning, 2018)
DP는 특정한 성격을 가진 알고리즘의 총합이다. 큰 문제를 작은 문제로 나누어 답을 구하는 기법 전반을 말한다. DP의 핵심은 '같은 계산을 두 번 하지 않는다'이다. 구현하는 방법에는 Top-down, Bottom-up 두 가지 방식이 있다. 하향식 방법은 메모이제이션(memoization)이라고 한다. 앞서 설명한 \(V_0(s)\), \(V_1(s)\)... 식으로 갱신하는 방식은 상향식 방법이다.
반복적 정책 평가 구현

두 칸짜리 그리드 월드를 예로 들어서 반복적 정책 평가 알고리즘의 흐름을 살펴보자.
이 환경에서 정책은 무작위 정책이고 상태 전이는 결정적이다. 따라서 가치 함수 갱신식을 다음과 같이 단순화 할 수 있다.

이제 정책 \(\pi\)의 가치 함수를 반복적 정책 평가 알고리즘으로 구현해보자. 우선 초기값으로 \(V_0(s)=0\)으로 셋팅한다. 두 칸짜리 그리드 월드에서 상태는 두 개 뿐이므로 다음과 같이 나타낸다.
$$V_0(L1) = 0, V_0(L2) = 0 $$
이제 백업 다이어그램을 보면서 \(V_1(s)\)을 갱신해보자.
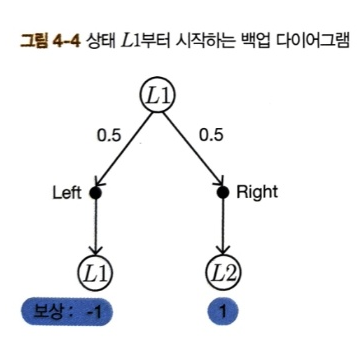
$$\begin{equation} \begin{split} V_1(L1) &= 0.5\{-1 + 0.9(V_0(L1)\} + 0.5\{1 + 0.9(V_0(L2)\} \\ &= 0.5(-1+0.9*0) + 0.5(1+0.9*0) = 0 \end{split} \end{equation}$$
$$\begin{equation} \begin{split} V_1(L2) &= 0.5\{0 + 0.9(V_0(L1)\} + 0.5\{-1 + 0.9(V_0(L2)\} \\ &= 0.5(0+0.9*0) + 0.5(-1+0.9*0) = -0.5 \end{split} \end{equation}$$

그림과 같이 \(V_0\)를 이용하여 \(V_1\)을 갱신했다. 이제 이 과정을 반복하면 된다. 코드로 구현하면 다음과 같다.

참고로 실제 가치 함수의 값은 [-2.25, -2.75]이다(랜덤 정책, 연립 방정식으로 푼 해). 결과를 보면 100번째 갱신 시점의 값이 거의 같은 값으로 수렴하는 것을 볼 수 있다.
더 큰 문제를 향해
이제 두 칸짜리 그리드 월드를 벗어나 3X4 그리드 월드를 풀어보자.
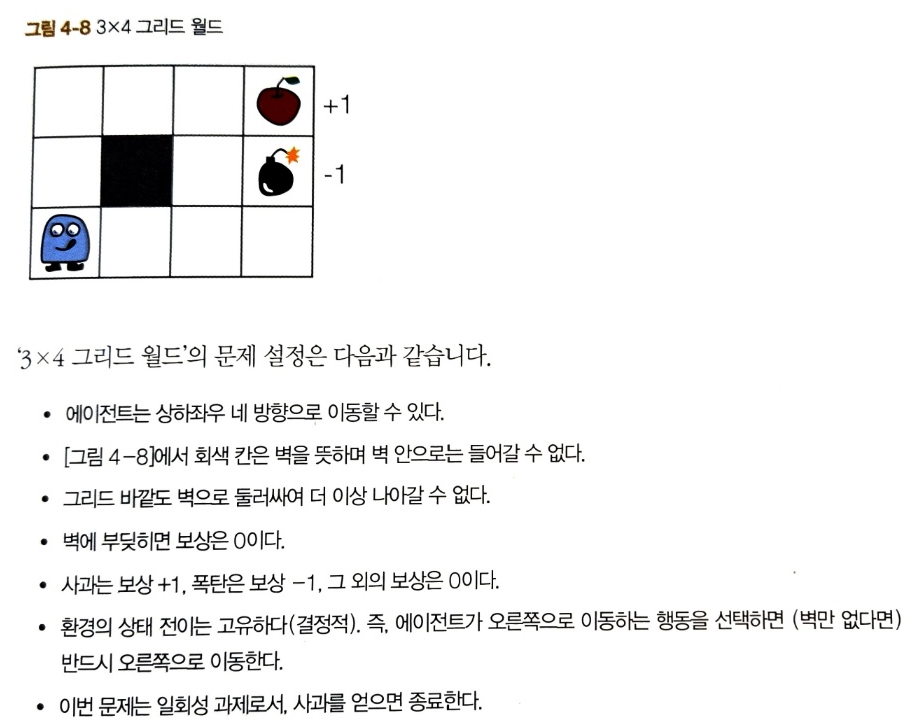
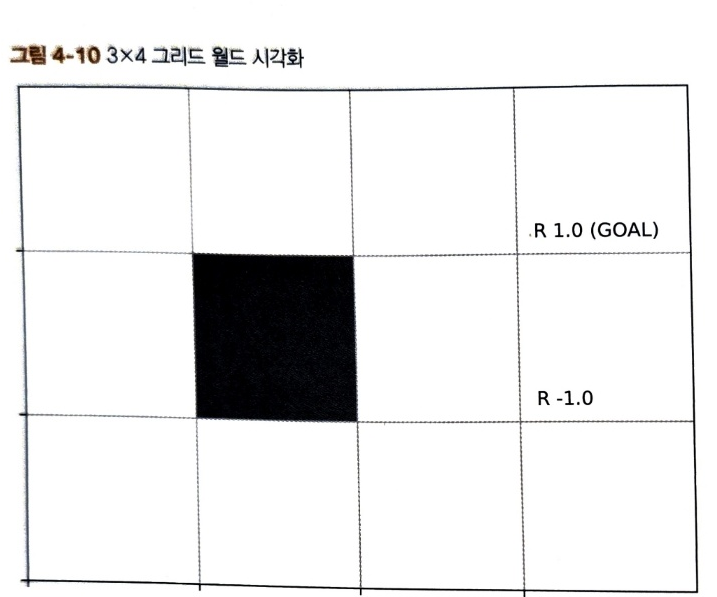
이번에는 그리드 월드를 시각화 해보자.


반복적 정책 평가 구현
다음과 같이 순차적으로 각 상태에 접근하도록 코드를 구현해보자.


3에서는 행동의 확률 분포를 가져온 뒤, 상태 전이 함수로 다음 상태를 얻는다. 그리고 4에서 이 정보들로 반복적 정책 평가 알고리즘의 갱신식을 갱신한다.
$$V_{k+1}=\sum_a \pi(a|s) {r(s,a,s') + \gamma V_k(s')}$$
이제 이 갱신을 반복한다. 매개변수 threshold 값보다 갱신된 양이 작아질 때까지 반복한다.

반복적 정책 평가 방법으로 무작위 정책을 평가하여 가치 함수를 구하면 다음 그림을 얻을 수 있다.

시작점인 맨 왼쪽 아래의 값이 -0.1인걸 보면 무작위로 움직일 경우, 사과(+1)보다 폭탄(-1)을 얻을 확률이 조금 더 크다고 할 수 있다.
DP를 적용하여 정책 평가의 실행 효율을 높일 수 있었다. 그러나 아직까지는 정책 평가만을 수행했을 뿐이다. 다음 절에서는 최적 정책을 찾는 방법에 대해서 알아보자.
[내가 헷갈렸던 부분]
'반복적 정책 평가'를 보면 정책을 통해서 행동을 수행하고 가치 함수를 업데이트 한다. 나는 이 부분에서 가치 함수가 업데이트 되기 때문에 뭔가 정책이 더 발전되고 있구나 라고 착각했었다. 하지만 가치가 업데이트 되도 정책은 변하지 않는다. 즉 이 정책이 얼마의 가치가 있는가를 반복적으로 평가만 하고 있을 뿐이다.
정책 반복법
언제나 최종 목표는 최적 정책 찾기이다. 벨만 최적 방정식을 만족하는 연립 방정식을 푸는 방법도 있었으나 계산량이 너무 많았다. 상태의 크기를 S, 행동의 크기를 A라고 한다면 \(A^S\)만큼의 계산이 필요하다. 그래서 문제가 조금만 복잡해져도 적용하기가 불가능하다.
이제 DP를 통해서 효율적으로 평가하는 것이 가능했으니 조금씩 정책을 변경해가면서 가치를 '비교'해보고 '개선'할 수 있다.
정책 개선
정책을 개선하는 힌트는 '최적 정책'에서 찾을 수 있다.
최적 정책 \(\mu_*\)는 다음 식으로 표현된다.
$$\mu_*(s)= \underset{a}{\operatorname{argmax}} q_*(s,a)$$ (4.4)
$$\mu_*(s)= \underset{a}{\operatorname{argmax}} \sum_{s'} p(s'|s, a) \{r(s,a,s') + \gamma v_*(s')\}$$
이 식에서 최적 정책은 \(\text{argmax}_a\)연산이 찾아준다. 이 연산은 국소적인 후보 중에서 최선의 행동을 선택하게 한다. '국소적'인 후보 중 선택하기 때문에 이 정책을 탐욕 정책(greedy policy)라고 한다.
위 식을 이용해서 최적 가치 함수 \(v_*\)를 알면 최적 정책 \(\mu_*\)를 구할 수 있다. 하지만 \(v_*\)를 알기 위해서는 최적 정책 \(\mu_*\)가 필요하다. 닭이 먼저냐 달걀이 먼저냐의 문제이다.
4.4는 최적 정책 \(\mu_*\)에 대한 식이지만, 여기서는 임의의 결정적 정책 \(\mu\)에 식 4.4를 적용해보자.
$$\mu'(s)= \underset{a}{\operatorname{argmax}} q_{\mu}(s,a)$$ (4.6)
$$\mu'(s)= \underset{a}{\operatorname{argmax}} \sum_{s'} p(s'|s, a) \{r(s,a,s') + \gamma v_\mu (s')\}$$ (4.7)
\(\mu'(s)\)는 새로운 정책을 뜻한다. 위 식에 의한 정책 갱신을 '탐욕화'라고 부를 수 있다. 탐욕화된 정책 \(\mu'(s)\)에는 재미난 특징이 있다. 모든 상태 s에서 현재 정책 \(\mu(s)\) 와 \(\mu'(s)\)가 같다면(정책이 그대로 라면) 정책 \(\mu(s)\)는 이미 최적 정책이라는 것이다. 왜냐하면 식 4.6에 의해 정책이 갱신되지 않는다면 다음 식을 만족하기 때문이다.
$$\mu(s) = \underset{a}{\operatorname{argmax}} q_\mu(s,a)$$
이 식은 최적 정책이 만족하는 그 자체이기 때문에 탐욕화를 수행해도 정책이 그대로라면 \(\mu(s)\)는 이미 최적 정책이라는 뜻이다.
그렇다면 탐욕화의 결과로 정책이 갱신되는 경우는 어떤 특징이 있을까? 정책 \(\mu'\)가 \(\mu\)와 달라진다면 새로운 정책은 항상 기존 정책보다 개선된다는 사실이 밝혀졌다. 더 구체적으로, 모든 상태 s에서 \( v_{\mu'}(s) \geq v_\mu(s)\)가 성립한다.
지금까지의 설명을 종합하면, 정책 탐욕화의 효과를 다음과 같이 정리할 수 있다.
- 정책이 항상 개선된다.
- 만약 정책이 개선(갱신)되지 않는다면 그 정책이 곧 최적 정책이다.
평가와 개선 반복
앞서서 정책 평가와 개선(탐욕화)를 알아보았다. 이 두 가지가 최적 정책을 찾는 방법의 핵심이다.

그림의 처리 과정을 글로 정리하면 다음과 같다.
- \(\pi_0\)를 초기화한다. 확률적일 수도 있으므로 \(\mu_0\)로 표기하지 않음.
- 정책 \(\pi_0\)의 가치 함수를 평가하여 \(V_0\)를 얻는다. 반복적 정책 평가 알고리즘을 사용한다.
- \(V_0\)를 이용하여 탐욕화를 수행한다(식 4.7을 이용하여 정책 갱신). 탐욕 정책은 언제나 하나의 행동을 선택하므로 결정적 정책인 \(\mu_1\)을 얻을 수 있다.
- 1~3 과정을 반복한다.
이 과정을 계속하면 탐욕화를 해도 정책이 더 이상 갠신되지 않는 지점에 도달한다. 그때의 정책이 바로 최적 정책이다(그리고 최적 가치 함수). 이렇게 평가와 개선을 반복하는 알고리즘을 정책 반복법(policy iteration)이라고 한다.
환경은 상태 전이 확률 \(p(s'|s,a)\) 와 보상 함수 \(r(s,a,s')\)로 표현된다. 강화 학습에서는 이 둘을 가리켜 '환경 모델' 또는 단순히 '모델'이라고 한다. 환경 모델이 알려져 있다면 에이전트는 아무런 행동 없이 가치 함수를 평가할 수 있다. 그리고 정책 반복법을 이용하면 최적 정책도 찾을 수 있다. 에이전트가 실제 행동을 하지 않고 최적 정책을 찾는 문제를 계획 문제(Planning)라고 한다. 이번 장에서 다루는 문제는 계획 문제이다. 반면 강화 학습은 환경 모델을 알 수 없는 상황에서 수행하는 경우가 많은데, 그럴 때는 에이전트가 실제로 행동을 취해 경험 데이터를 쌓으면서 최적 정책을 찾는다.
(DP방식이 Planning에 적합하다고 봐야하나?)
정책 반복법 구현
앞에서 정책 평가를 살펴봤으니 이제 정책 개선을 살펴보자.

정책 개선
정책을 개선하기 위해서는 현재의 가치 함수에 대한 탐욕 정책을 구한다. 수식으로는 다음과 같다.
$$\mu'(s) = \underset{a}{\operatorname{argmax}} \sum_{s'} p(s'|s,a) \{r(s,a,s') + \gamma v_\mu (s') \}$$
이번 문제에서는 결정적 상태 변화 환경이므로 탐욕화를 다음과 같이 단순화 할 수 있다.
$$\mu'(s) = \underset{a}{\operatorname{argmax}} \{r(s,a,s') + \gamma v_\mu (s') \}$$ (4.8)
가치 함수를 탐욕화하는 함수를 구현하면 다음과 같다.

1에서는 각 행동을 대상으로 식 4.8의 \(r(s, a, s') + \gamma v_\pi(s')\)을 계산한다. 그리고 2에서는 argmax를 통해 가치 함수 값이 가장 큰 행동을 찾은 다음 max_action이 선택될 확률을 1.0으로 조정한다. 3에서 이를 상태에서 취할 수 있는 행동의 확률 분포로 설정한다.
평가와 개선 반복
이제 평가와 개선을 반복하는 정책 반복법을 구현할 준비가 되었다.

먼저 정책 pi와 v를 초기화 한다. 그리고 1에서 현재의 정책을 평가하여 V를 얻고 2에서 V를 기반으로 탐욕화된 정책 new_pi를 얻는다. 3에서 갱신 여부를 확인하고 갱신되지 않았으면 loop를 빠져나온다.
다음 코드를 실행하고 단계별 시각화를 해보면 아래와 같다.


네 번째 갱신 후에는 모든 칸에서 폭탄을 피하고 사과를 얻는 방향으로 향하고 있다.
3X4 그리드 월드 문제에서 결정적 최적 정책은 두 가지가 있다. 하나는 위 그림처럼 움직이는 것이고 다른 하나는 시작 지점(왼쪽 맨 아래 칸)에서 '위'로 이동하는 정책이다. 어느 쪽을 선택하든 최단 시간에 골인할 수 있다.
가치 반복법
앞에서는 정책 반복법을 통해서 최적 청잭을 찾았다.

'평가' 단계에서는 정책을 평가하여 가치 함수를 얻는다. 그리고 '개선' 단계에서는 가치 함수를 탐욕화하여 개선된 정책을 얻는다. 이를 번갈아 반복하면 최적 정책 \(\mu_*\)와 최적 가치 함수 \(v_*\)에 점점 가까워진다. 이 과정을 그림으로는 다음처럼 표현 가능하다.
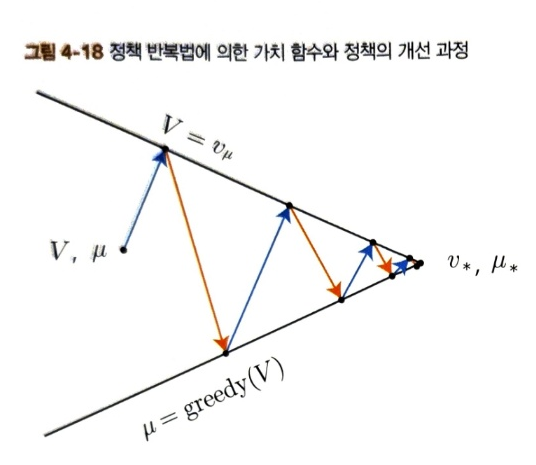
위 그림에서는 가치 함수 V와 정책 \(\mu\)가 취할 수 있는 공간이 2차원으로 표현되어있다. 본래는 다차원적이고 복잡한 공간이지만 직관적으로 이해하기 위해 단순화 되었다. 정책 반복법은 '평가'와 '개선'을 번갈아 반복한다. 평가 단계에서는 위쪽 직선으로 이동하고 개선 단계에서는 V를 탐욕화한다. 이 두 작업을 반복하면 결국 두 직선이 만나는 \(v_*, \mu_*\)에 도달하게 된다.

하지만 목표에 도달하기 위해서 위 그림처럼 여러가지 변형이 있을 수 있다. 위 그림처럼 평가와 개선을 완전히 끝내기 전에 다음 단계로 전환하는 것을 일반화한 정책 반복(generalizaed policy iteration)이라고 한다. 임계값을 통해 얼마든지 자유롭게 변경할 수 있다.
정책 반복법에서는 평가와 개선을 각각 최대한으로 번갈아 수행한다. 그렇다면 평가와 개선을 각각 '최소한'으로 수행하면 어떻게 될까? 이것이 바로 가치 반복법(value iteration)의 아이디어이다.
가치 반복법 도출
가치 반복법을 알아보기 전에 정책 반복법을 다시 한번 정리해 보자.

그림과 같이 모든 상태의 가치 함수를 여러번 갱신한다. 이 갱신작업이 수렴되면 '개선(탐욕화)' 단계로 넘어간다. 이와 대조적으로 가치 반복법의 핵심 아이디어는 하나의 상태만 딱 한 번 갱신하고 곧바로 '개선' 단계로 넘어가는 것이다.

위 그림에서처럼 상태 하나만 개선하고 곧장 평가 단계로 넘어간다. 평가 단계에서도 해당 상태 하나의 가치 함수를 한 번만 갱신한다. 그 다음 다음 위치를 개선하고 평가하는 흐름으로 진행된다. (위 그림에서는 개선 단계부터 시작했지만 개선과 평가는 번갈아 진행되므로 어느 단계를 먼저 진행하든 상관없음)
이 아이디어를 수식으로 나타내보자. 개선 단계에서 하는 탐욕화는 수식으로 다음과 같이 쓸 수 있다.
$$\mu(s) = \underset{a}{\operatorname{argmax}} \sum_{s'} p(s'|s,a){r(s,a,s') + \gamma V(s')}$$
현재의 가치 함수는 V(s)이다.
다음은 정책 평가 단계(가치 함수 업데이트)이다. 갱신 전의 가치 함수를 V(s), 갱신 후의 가치 함수를 V'(s)라고 하면 DP에 의한 갱신 식은,
$$V'(s) = \sum_{a, s'} \pi(a|s) p(s'|s,a) \{r(s,a,s') + \gamma V(s')\}$$
여기서 \(\pi(a|s)\)가 확률적으로 표기되어 있으나 '개선'단계를 한번 거치면 정책이 탐욕정책(argmax에 의해)으로 바뀌게 되므로 결정적 정책 \(\mu(s)\)로 취급하여 단순화하여 표기할 수 있다.
$$V'(s) = \sum_{s'} p(s'|s,a) \{r(s,a,s') + \gamma V(s')\}$$
이것이 '평가' 단계의 가치 함수 갱신식이다. 이제 개선과 평가 단계의 계산을 나란히 써보면,

위 그림에서 보듯 개선과 평가 단계에서 똑같은 계산이 중복됨을 알 수 있다. 더 정확하게 말하자면 개선 단계에서 탐욕 행동을 찾기 위해 계산을 한 후, 평가 단계에서 그 탐욕 행동을 이용하여 똑같은 계산을 다시 수행한다. 이 중복된 계산은 다음처럼 하나로 묶을 수 있다.
$$V'(s) = \underset{a}{\operatorname{max}} \sum_{s'} p(s'|s,a) \{r(s,a,s') + \gamma V(s')\}$$ (4.11)
위 식에서는 최대값을 찾아주는 max 연산자를 사용하여 가치 함수를 직접 갱신한다.
위 식에서 주목할 점은 바로 정책 \(\mu\)가 등장하지 않는다는 것이다. 즉, 정책을 사용하지 않고 가치 함수를 갱신하고 있다. 그래서 위 식을 활용하여 최적 가치 함수를 구하는 알고리즘을 '가치 반복법'이라고 한다. 가치 반복법은 이 하나의 식만을 이용하여 '평가'와 '개선'을 동시에 수행한다.
벨만 최적 방정식의 수식은 다음과 같다.
$$v_*(s)= \underset{a}{\operatorname{max}} \sum_{s'}p(s'|a,s)\{r(s,a,s') + \gamma v_*(s')\}$$
벨만 최적 방정식과 식 4.11을 비교해보면 4.11은 벨만 최적 방정식을 '갱신식'으로 표현한 것임을 알 수 있다.
또한 식 4.11의 갱신식을 다음 형태로도 표현할 수 있다.
$$V_{k+1}(s)= \underset{a}{\operatorname{max}} \sum_{s'} p(s'|a,s) \{r(s,a,s') + \gamma V_k(s')\}$$
이와 같이 가치 반복법은 k=0부터 시작하여 k=1, 2, 3, ... 순서대로 가치 함수 \(V_k\)를 갱신하는 알고리즘으로, DP의 특징인 같은 계산을 두 번 하지 않는다는 조건을 만족한다.
가치 반복법으로 갱신을 무한히 반복하면 최적 가치 함수를 얻을 수 있다. 하지만 현실에서는 무한히 반복할 수 없으므로 임계값을 설정하여 갱신량이 임계값 밑으로 떨어지면 갱신을 중단한다.
\(V_*(s)\)가 주어지면 최적 정책은 다음과 같다
$$\mu_*(s) = \underset{a}{\operatorname{argmax}} \sum_{s'}p(s'|a,s)\{r(s,a,s') + \gamma V_*(s')\}$$
가치 반복법 구현

정책 반복법과 달리 한번만 갱신하는 value_iter_onestep() 함수를 갱신이 수렴할 때까지 호출하면 된다.
정리
이번 장에서는 동적 프로그래밍을 이용하여 최적 정책을 구하는 방법을 배웠다. 그것이 정책 반복법과 가치 반복법이다.
정책 반복법은 '평가'와 '개선'이라는 두 과정을 번갈아 반복한다. 평가 단계에서는 DP를 이용해 가치 함수를 평가하고 그 가치 함수를 탐욕화하여 정책을 개선한다. 만약 더 이상 개선되지 않으면 그 정책이 곧 최적 정책이다.
가치 반복법은 평가와 개선을 한 번에 수행한다. 수식 하나만으로 가치 함수를 갱신하고 이 갱신을 반복하여 최적 가치 함수를 찾는다. 최적 가치 함수를 찾으면 최적 정책도 찾을 수 있다.
$$V_{k+1}(s)= \underset{a}{\operatorname{max}} \sum_{s'} p(s'|a,s) \{r(s,a,s') + \gamma V_k(s')\}$$
'인공지능 > [책] 밑바닥부터 시작하는 딥러닝4' 카테고리의 다른 글
| Chapter 6. TD법(SARSA, Q-learning) (0) | 2025.01.15 |
|---|---|
| Chapter 5. 몬테카를로 법 (0) | 2025.01.14 |
| Chapter 3. 벨만 방정식 (0) | 2025.01.09 |
| Chapter 2. 마르코프 결정 과정 (0) | 2025.01.08 |
| Chapter 1. 밴디트 문제 (0) | 2025.01.06 |

